Sonderfälle bei der Implementierung von CSS-Eckenformen in Blink

Noam Rosenthal

Veröffentlicht am 19. Februar 2026

Eine der CSS-Funktionen, die 2025 in Chrome eingeführt wurden, war corner-shape. Damit können Sie die Form einer Ecke mit einem border-radius mithilfe von Keywords wie bevel und scoop definieren. Sie können auch eine superellipse-Funktion verwenden, die einen Wert zwischen -Infinity und Infinity empfängt.

Einen guten Überblick über das Feature und seine Funktionsweise bietet dieser ausführliche Artikel von Amit Sheen bei Frontend Masters.

Bei der Implementierung dieser Funktion Anfang 2025 bin ich auf einige interessante Herausforderungen unterschiedlicher Komplexität gestoßen. Ich habe viel über Superellipsen, das Malen von Rändern in Blink und die Verwendung von Vektormathematik für 2D-Grafiken gelernt.

In diesem Dokument teile ich einige der Dinge, die ich gelernt habe und die auch für andere interessant sein könnten.

Symmetrie konvexer und konkaver Formen

Während superellipse-Werte (k) traditionell zwischen 0 und Infinity liegen, wobei Werte zwischen 0 und 1 konkav und die restlichen Werte konvex sind (1 ist bevel), liegen superellipse-Werte in der CSS-Spezifikation zwischen -Infinity und Infinity und stellen 2k dar. Dadurch wird eine Symmetrie erzeugt, da jeder positive Wert wie das Spiegelbild seines negativen Gegenstücks aussieht.

Standardmäßig funktioniert die Formel superellipse jedoch nicht so.

Die Formel für superellipse lautet: xk + yk = 1. Die inverse Formel x1/k + y1/k = 1 erzeugt keine visuell symmetrische Kurve.

Beispiel mit einem k von 2:

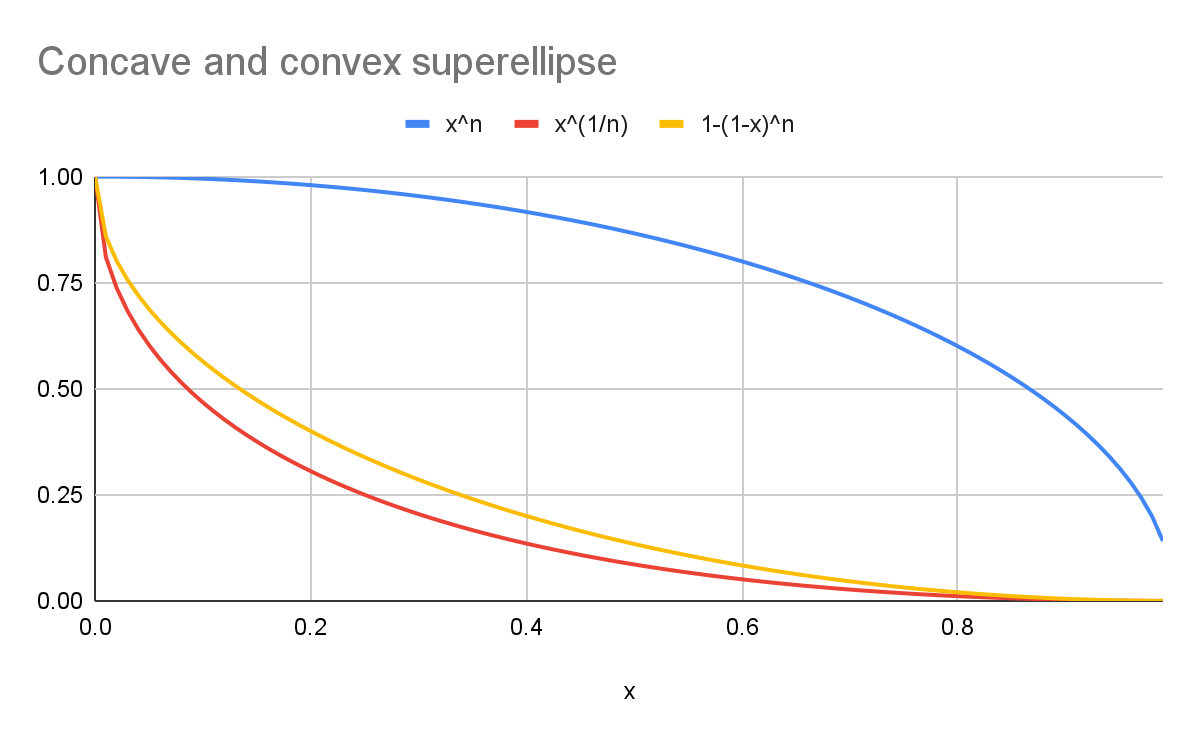
Vergleich von Superellipsenkurven: runde Superellipse (blau), Superellipse mit der kanonischen Formel (rot) und visuell symmetrische Kurve (gelb).
  • Die blaue Kurve stellt eine Runde superellipse (y=xn) dar.
  • Die rote Kurve stellt eine scoop-superellipse mit der kanonischen Formel (y=x1/n) dar.
  • Die gelbe Kurve stellt eine Kurve dar, die visuell symmetrisch zur blauen Kurve (y=1-(1-x)n) ist.

Wie das Diagramm zeigt, sind die Formen nicht identisch.

Ich werde nicht näher auf die Mathematik eingehen, aber es hat mit dualen Normen und der Art und Weise zu tun, wie wir Krümmung wahrnehmen.

In Bezug auf die Spezifikation und Implementierung stellen wir hier etwas Visuelles dar. Daher verwenden wir die symmetrischen Äquivalente, wenn wir konkave Formen berechnen. Die restlichen Berechnungen werden für konvexe Formen (k>=1 oder positive Superellipse-Werte) durchgeführt.

Formel in geschlossener Form

Die nächste Herausforderung besteht darin, die Kurve oder den Umfang des superellipse in geschlossener Form darzustellen, also mit einer Formel, die aus einfachen arithmetischen Operationen besteht. Das ist für die Leistung unerlässlich, da das System so das superellipse-Rendering an die Grafik-Engine übergeben kann.

Grafik-Engines wie Skia sind mit Bézierkurven vertraut. Wenn Sie also eine superellipse mit einer kleinen Anzahl von Bézierkurven darstellen, die ihren Umfang annähern, wird das Rendern einer superellipse-Kurve leistungsfähiger.

Glücklicherweise können wir mit der symbolischen Regression eine Formel finden, die eine halbe konvexe Ecke als einzelne kubische Bézierkurve darstellt.

Eine kubische Bézierkurve hat vier Punkte:

  • Der erste Punkt ist (0, 1).
  • Der letzte Punkt ist die tatsächliche halbe Ecke der Superellipse: 0.51/k,0.51/k.
  • Der erste Kontrollpunkt wird auf derselben Höhe wie der Startpunkt gedehnt: (a, 1).
  • Der zweite Kontrollpunkt liegt diagonal zur halben Ecke: (0.51/k - b,0.51/k + b).

Der hier verwendete Wert für die halbe Ecke ist eine sehr wichtige Koordinate, die wir später für andere Berechnungen verwenden werden.

Dabei werden a und b aus k mithilfe der symbolischen Regression berechnet.

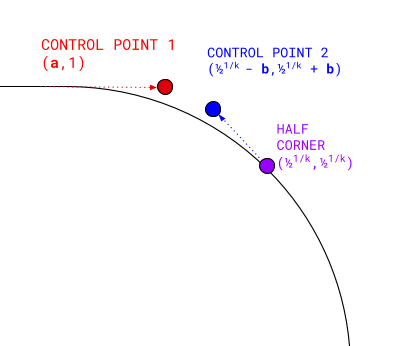
Abbildung der auf eine Kurve abgebildeten Kontrollpunkte.
Eine Demonstration finden Sie in diesem Codepen.

Wenn Sie diese vier Punkte berechnen und eine kubische Bézierkurve zwischen ihnen rendern, erhalten Sie eine geschlossene konvexe halbe Ecke mit einem bestimmten k. Wir können die Ergebnisse dann drehen, um den Rest der Ecke zu füllen, sie auf andere Ecken anwenden und spiegeln, um die konkaven Entsprechungen zu rendern.

Ohne weiter in die mathematischen Details einzugehen, lautet die Formel zur Berechnung von a und b so:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

Rahmen und Schatten

Das System berechnet nicht nur den Pfad des Eckenumfangs, sondern auch, wie er aussieht, wenn er nach innen (als Rahmen oder als box-shadow) oder nach außen (als outline oder als normales box-shadow) versetzt wird. In herkömmlichen Grafikbibliotheken wird dies durch Strichzeichnungen erreicht.

Ränder und Schatten in CSS haben jedoch Rendering-Eigenschaften, die sich von Strichen unterscheiden:

  • Die Ränder sind nicht einheitlich.
  • Beispielsweise kann der obere Rahmen 10 Pixel und der rechte Rahmen 5 Pixel breit sein. Die Ecke wird dann entsprechend interpoliert.
  • Außerdem verlaufen sie nach innen statt nach beiden Seiten.
  • Schatten und Konturen werden nicht genau wie ein Strich gerendert.
  • Stattdessen werden sie so angepasst, dass die Ecken scharf dargestellt werden.

Der übliche Rendering-Pfad für Rahmen und Schatten hat bei corner-shape-Werten, die rund oder konvexer als corner-shape sind (z. B. squircle), gut funktioniert. Er kann auch um 90 Grad gedreht werden, um Formen zu rendern, die konkav sind (z. B. scoop). Für corner-shape-Werte zwischen -1 und 1 funktioniert er jedoch nicht, da durch das Versetzen des Rahmens oder Schattens parallel zur Kante eine Ecke entsteht, die eine ungleichmäßige Breite aufweist.

Wenn Sie beispielsweise eine bevel-Ecke nehmen und den Rahmen um einige Pixel nach beiden Seiten versetzen, entsteht ein „Bauch“-Effekt, bei dem die Mitte der Ecke breiter als die Seiten aussieht.

Um das zu berücksichtigen, soll ein Effekt erstellt werden, der wie ein Strich funktioniert. Dazu wird die Normale der Eckkurve am Anfang ermittelt und so lang gemacht wie die Breite von border oder shadow-spread.

Glücklicherweise ist dies nur für Unterellipsen (zwischen bevel und round) erforderlich, da Hyperellipsen wie squircle wie erwartet funktionieren.

Um die Normale einer Subellipse zu finden, genügt es, die Normale der entsprechenden quadratischen Kurve zu finden, da Subellipsen und ihre quadratischen Kurvenäquivalente nahe beieinander liegen.

Mithilfe der zuvor berechneten halben Ecke können Sie eine quadratische Kurve mit demselben Mittelpunkt finden, ihren quadratischen Kontrollpunkt ableiten und daraus die Normale berechnen.

Die Normale wird mit derselben Länge wie border-width oder shadow-spread fortgesetzt und die resultierende Kurve wird dann mit den Kanten (innere Kante für den Rahmen, äußere Kante für den Schatten) beschnitten, um einen durchgehenden Pfad zu erstellen.

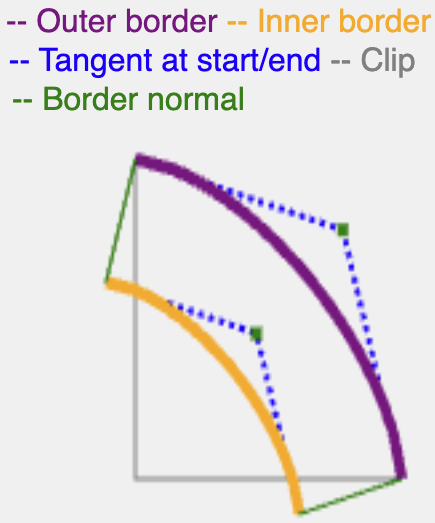
Abbildung einer Ecke mit einem Rahmen, die zeigt, wie die Normale verlängert wird, um die Rahmenform zu definieren.
Dieses Beispiel auf CodePen ansehen.

Es gibt mathematisch genauere Methoden, um eine Tangente für ein superellipse zu berechnen, aber diese Methode ist effizient und liefert angemessene Ergebnisse für das Rendern von Rändern und Schatten.

Farbfugen

Ein interessanter Teil des Renderns in Browsern ist in CSS nicht angegeben. Damit werden Rahmen mit nicht einheitlichen Farben oder Stilen gerendert. Beispiel: Ihr Element hat einen grünen durchgezogenen oberen Rahmen und einen gelben gepunkteten rechten Rahmen. In diesen Fällen ist die Gehrung eine Schnittlinie zwischen der entsprechenden Ecke des Rahmenrands und der entsprechenden Ecke des Innenabstands. Sie bildet die Grenze zwischen den angrenzenden Kanten.Obwohl sie nicht angegeben ist, ist die Darstellung in den verschiedenen Browsern einigermaßen konsistent.

In Blink (und anderen Browsern) wird dies so implementiert: Die Kante, die gleich gerendert wird, wird grob wie ein Polygon beschnitten, das sich am Gehrungspunkt kreuzt. Sie wird so berechnet, dass sie die relevante Kante, aber keine der anderen Kanten enthält. So wird Ausbluten vermieden, bei dem eine der anderen Kanten mit dem falschen Stil und der falschen Farbe gerendert wird.

Bisher war die Berechnung dieses Polygons relativ einfach, da sich die Eckbereiche bei regulären abgerundeten Ecken nie überschneiden können. Bei Hypo-Ellipsen und insbesondere bei konkaven Superellipsen (negative superellipse-Werte) ändert sich dies jedoch. Dadurch können sehr interessante Formen entstehen, die die naiven Schnittmengenpolygone sehr anfällig für Überschneidungen und „Ausbluten“ machen.

Betrachten Sie das folgende CSS:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}
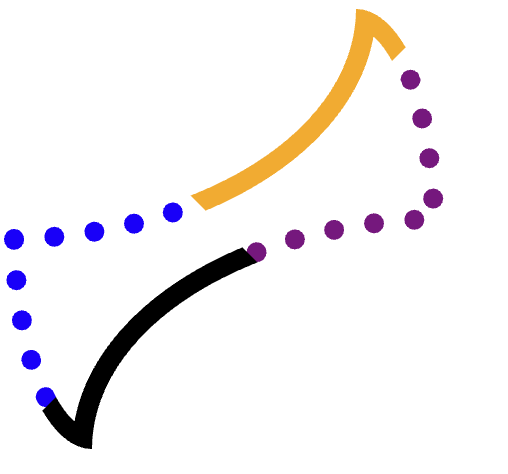
Beispiel für ein CSS-Element mit nicht einheitlichen Rändern: orange, lila gepunktet, schwarz und blau gepunktet.

Wir möchten jede Kante (orange, lila gepunktet, schwarz, blau gepunktet) separat zuschneiden und dann den Pfad zeichnen.

Dazu ist ein sorgfältiges Zuschneiden erforderlich, damit keine der drei anderen Ecken überlappt wird.

Sehen Sie sich beispielsweise die orangefarbene (obere) Kante an.

Es ist schwierig, ein genaues Polygon zu finden, das die gesamte Kante umfasst, ohne in die violetten, gelben oder sogar schwarzen Kanten überzugehen. Andere Formen sind schwieriger.

Dazu sind drei Clips erforderlich.

Der erste Clip enthält die gesamte Kante mit der vollen Ecke (ohne Gehrung). Beispiel:

Eine abgeschnittene Ecke, die zwei Ecken darstellt (eine abgerundete und eine mit einer Aussparung).

Sie besteht aus zwei Ecken (eine scoop, eine rund), die an den Enden verbunden sind und zwischen denen sich eine minimale Kante befindet.

Wenn Sie mit dieser Form beginnen, werden Überschneidungen mit der gegenüberliegenden Kante vermieden. Jetzt sind nur noch die beiden Gehrungen ein Problem.

Dazu wird ein Polygon aus dieser Ecke herausgeschnitten, das zwischen den Ecken des Rahmens und des Innenabstands verläuft und stoppt, sobald es sich mit dem Rahmen schneidet:

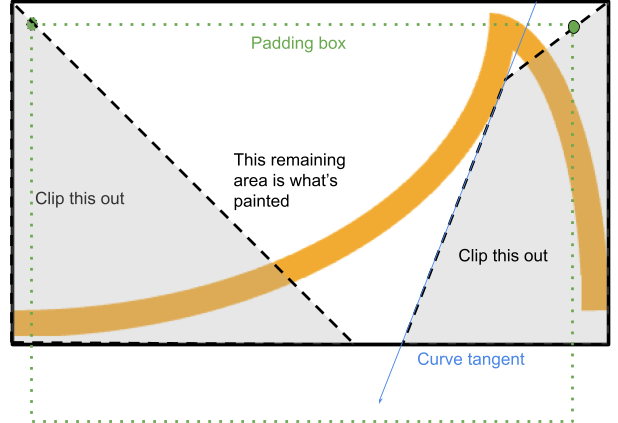
Eine Demonstration der Bereiche, die beschnitten werden sollen.

Das System ermittelt den Punkt, an dem sich eine Linie von der Rahmenkante zur Padding-Kante mit der Tangente der Kurve vom relevanten Startpunkt aus schneidet (wenn die Kurve konkav ist).

Wenn dieser Punkt innerhalb des gerenderten Bereichs liegt, wird der Vorgang dort angehalten und entlang dieser Tangente fortgesetzt, bis er wieder auf die Grenzbox trifft. So wird ein Viereck fertiggestellt.

Andernfalls kann ein einfaches Dreieck beschnitten werden.

Zusammenfassung

Die Webplattform bietet Webdesignern und ‑entwicklern viele Möglichkeiten. Manchmal verbirgt sich hinter einer CSS-Eigenschaft, die einen einzelnen numerischen Wert akzeptiert, eine erhebliche Komplexität, damit sie korrekt und konsistent gerendert wird.

Die Funktion corner-shape war überraschend komplex. Diese Dokumentation soll zukünftigen Entwicklern helfen, die an dieser Funktion in Blink, anderen Browsern oder der Spezifikation arbeiten.