กรณีข้อยกเว้นของการใช้รูปร่างมุม CSS ใน Blink

Noam Rosenthal

เผยแพร่: 19 กุมภาพันธ์ 2026

ฟีเจอร์ CSS อย่างหนึ่งที่ Chrome เปิดตัวในปี 2025 คือ corner-shape ซึ่งช่วยให้คุณกำหนดรูปร่างของมุมที่มี border-radius ได้โดยใช้ คีย์เวิร์ด เช่น bevel และ scoop นอกจากนี้ คุณยังใช้ฟังก์ชัน superellipse ที่รับค่าระหว่าง -Infinity ถึง Infinity ได้ด้วย

ดูภาพรวมที่ยอดเยี่ยมของฟีเจอร์และวิธีการทำงานได้ในบทความที่ครอบคลุมของ Amit Sheen ที่ Frontend Masters

เมื่อใช้ฟีเจอร์นี้ในช่วงต้นปี 2025 ฉันพบความท้าทายที่น่าสนใจ 2-3 อย่างที่มีความซับซ้อนแตกต่างกัน ฉันได้เรียนรู้มากมายเกี่ยวกับ วงรีไฮเปอร์ การวาดเส้นขอบใน Blink และการใช้คณิตศาสตร์เวกเตอร์สำหรับกราฟิก 2 มิติ

เอกสารนี้จะแชร์สิ่งที่ฉันได้เรียนรู้มา ซึ่งอาจเป็นสิ่งที่น่าสนใจสำหรับคนอื่นๆ ด้วย

สมมาตรของรูปร่างนูนและเว้า

แม้ว่าค่า superellipse (k) จะอยู่ระหว่าง 0 ถึง Infinity โดยที่ ค่าระหว่าง 0 ถึง 1 จะเป็นเว้า และค่าที่เหลือจะเป็นนูน (1 คือ bevel) ค่า superellipse ในข้อกำหนด CSS จะอยู่ระหว่าง -Infinity ถึง Infinity และ แสดงถึง 2k ซึ่งจะสร้างความสมมาตรเนื่องจากค่าบวกใดๆ จะดูเหมือน ภาพมิเรอร์ของค่าลบที่สอดคล้องกัน

อย่างไรก็ตาม โดยค่าเริ่มต้น สูตร superellipse จะไม่ทำงานแบบนั้น

superellipseสูตรคือ xk + yk = 1 สูตรผกผัน x1/k + y1/k = 1 ไม่สร้างเส้นโค้งที่สมมาตรด้วยสายตา

เช่น หากมี k ของ 2

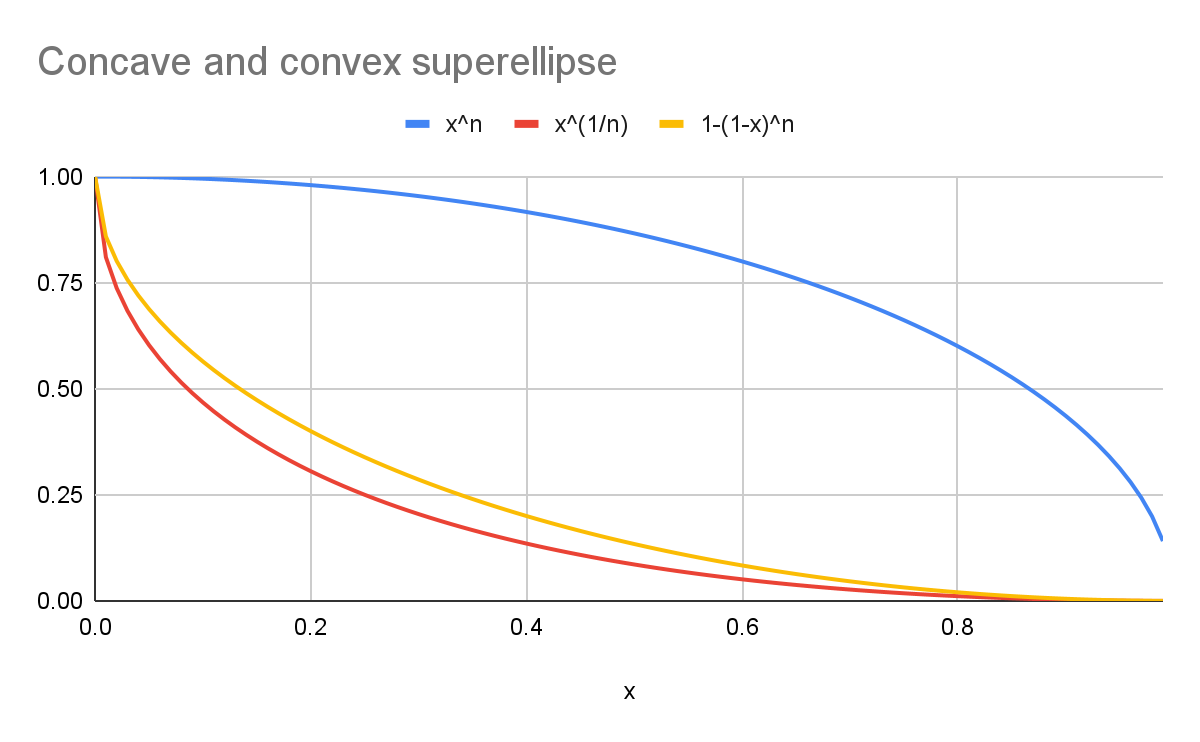
• เส้นโค้งสีน้ำเงินแสดงรอบ superellipse (y=xn)
• เส้นโค้งสีแดงแสดงถึง scoop superellipse ที่มีสูตร Canonical (y=x1/n)
• เส้นโค้งสีเหลืองแสดงเส้นโค้งที่สมมาตรกับเส้นโค้งสีน้ำเงิน (y=1-(1-x)n)

ดังที่แผนภูมิแสดง รูปร่างทั้ง 2 ไม่เหมือนกัน

ฉันจะไม่เจาะลึกเรื่องคณิตศาสตร์ แต่เรื่องนี้เกี่ยวข้องกับบรรทัดฐานคู่และ วิธีที่เรารับรู้ความโค้ง

ในแง่ของข้อกำหนดและการใช้งาน เราจะแสดงภาพบางอย่างที่นี่ ดังนั้นเราจึงใช้ค่าสมมาตรที่เทียบเท่ากันเมื่อคำนวณรูปร่างเว้า ส่วนที่เหลือของการคำนวณจะทำกับรูปร่างนูน (k>=1 หรือค่า Superellipse ที่เป็นบวก)

สูตรแบบปิด

ความท้าทายถัดไปคือการแสดงเส้นโค้งหรือขอบเขตของsuperellipseในรูปแบบปิด ซึ่งเป็นสูตรที่สร้างขึ้นจากการดำเนินการทางคณิตศาสตร์อย่างง่าย ซึ่งเป็นสิ่งจำเป็นสำหรับประสิทธิภาพที่ช่วยให้ระบบส่งต่อsuperellipseการแสดงผลไปยังเครื่องมือด้านกราฟิก

เอนจินกราฟิก เช่น Skia คุ้นเคยกับเส้นโค้งเบซิเยร์ ดังนั้นการแสดง superellipse ด้วยเส้นโค้งเบซิเยร์จำนวนเล็กน้อยที่ ประมาณขอบเขตของเส้นโค้งจะทำให้การแสดงผลเส้นโค้ง superellipse มีประสิทธิภาพมากขึ้น

โชคดีที่การใช้การถดถอยเชิงสัญลักษณ์ช่วยให้เราพบสูตรที่แสดงมุมนูนครึ่งหนึ่งเป็นเส้นโค้ง Bezier แบบลูกบาศก์เดียว

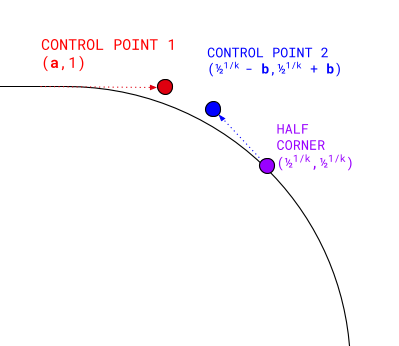
เส้นโค้ง Cubic Bezier มี 4 จุด ดังนี้

• จุดแรกคือ (0, 1)
• จุดสุดท้ายคือครึ่งมุมของวงรีซูเปอร์จริง: 0.51/k,0.51/k
• จุดควบคุมแรกจะยืดเข้าที่ระดับเดียวกับจุดเริ่มต้น (a, 1)
• จุดควบคุมที่ 2 อยู่ในแนวทแยงมุมครึ่งมุม: (0.51/k - b,0.51/k + b)

ค่าครึ่งมุมที่ใช้ที่นี่เป็นพิกัดที่สำคัญมากซึ่งเราจะใช้ในการคำนวณอื่นๆ ในภายหลัง

โดย a และ b จะคำนวณจาก k โดยใช้การถดถอยเชิงสัญลักษณ์

หากต้องการดูการสาธิต โปรดดู Codepen นี้

การคำนวณจุดทั้ง 4 นี้และการแสดงผลเส้นโค้งเบซิเอร์แบบลูกบาศก์ระหว่างจุดเหล่านี้จะให้มุมครึ่งวงกลมแบบนูนที่ปิดด้วย k ที่กำหนด จากนั้นเราจะหมุนผลลัพธ์เพื่อเติมเต็มมุมที่เหลือ ใช้กับมุมอื่นๆ และพลิกเพื่อ แสดงผลมุมเว้าที่เทียบเท่า

สูตรในการคำนวณ a และ b มีดังนี้

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

เส้นขอบและเงา

นอกจากการคำนวณเส้นทางของขอบเขตมุมแล้ว ระบบยังคำนวณลักษณะของมุมเมื่อออฟเซ็ตเข้าด้านใน (เส้นขอบหรือขอบด้านใน box-shadow) หรือ ออกด้านนอก (outline หรือ box-shadow ปกติ) ด้วย ในไลบรารีกราฟิกทั่วไปจะใช้วิธีการลากเส้น

อย่างไรก็ตาม เส้นขอบและเงาใน CSS มีลักษณะการแสดงผลที่แตกต่างจากการลากเส้น ดังนี้

• ขอบไม่สม่ำเสมอ
• เช่น ขอบด้านบนอาจเป็น 10 พิกเซลและ ขอบด้านขวา 5 พิกเซล โดยมุมจะอยู่ระหว่างขอบทั้ง 2
• นอกจากนี้ ยังจะงอเข้าด้านในแทนที่จะงอไปทั้ง 2 ด้าน
• เงาและเส้นขอบจะไม่แสดงผลเหมือนเส้นขีด
• แต่จะปรับให้มุมดูคมชัดแทน

แม้ว่าเส้นทางการแสดงผลขอบและเงาตามปกติจะใช้ได้ดีกับค่า corner-shape ที่กลมหรือนูนกว่านั้น (เช่น squircle) และหมุนได้ 90 องศาสำหรับรูปร่างที่เว้ามากกว่า scoop แต่ค่าเริ่มต้นนี้ใช้ไม่ได้กับค่า corner-shape ระหว่าง -1 ถึง 1 เนื่องจากออฟเซ็ตขอบหรือเงาขนานกับขอบจะทำให้เกิดมุมที่ดูเหมือนมีความกว้างไม่สม่ำเสมอ

เช่น การใช้bevelมุมและออฟเซ็ตเส้นขอบด้วยพิกเซลบางส่วนไปทั้ง 2 ด้านจะสร้างเอฟเฟกต์ "โค้ง" ซึ่งตรงกลางของมุมจะดูกว้างกว่าด้านข้าง

เป้าหมายคือการสร้างเอฟเฟกต์ที่ทำงานเหมือนเส้นขีด โดยค้นหา เส้นตั้งฉากของเส้นโค้งมุมที่จุดเริ่มต้น และทำให้ยาวเท่ากับความกว้างของ border หรือ shadow-spread

โชคดีที่การดำเนินการนี้จำเป็นสำหรับเครื่องหมายจุดไข่ปลาแบบย่อย (ระหว่าง bevel และกลม) เท่านั้น เนื่องจากเครื่องหมายจุดไข่ปลาแบบไฮเปอร์ เช่น squircle ทำงานได้ตามที่คาดไว้

หากต้องการหาเส้นตั้งฉากของเส้นโค้งวงรีรอง ก็เพียงแค่หาเส้นตั้งฉากของเส้นโค้งกำลังสองที่สอดคล้องกัน เนื่องจากวงรีรองและเส้นโค้งกำลังสองที่เทียบเท่าอยู่ใกล้กัน

การใช้ครึ่งมุมเดียวกันที่คำนวณไว้ก่อนหน้านี้จะช่วยให้คุณค้นหาเส้นโค้งกำลังสองที่มีจุดกึ่งกลางเดียวกัน อนุมานจุดควบคุมกำลังสอง และคำนวณเวกเตอร์ปกติจากจุดนั้นได้อย่างง่ายดาย

เส้นปกติจะมีความยาวเท่ากับ border-width หรือ shadow-spread จากนั้นจะตัดเส้นโค้งที่ได้ด้วยขอบ (ขอบด้านในสำหรับเส้นขอบ ขอบด้านนอกสำหรับเงา) เพื่อสร้างเส้นทางต่อเนื่อง

ดูตัวอย่างนี้ใน CodePen

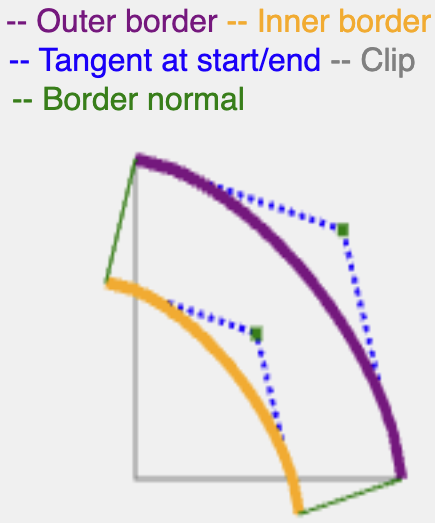
มีวิธีคำนวณแทนเจนต์สำหรับ superellipse ที่แม่นยำกว่าในเชิงคณิตศาสตร์ แต่วิธีนี้มีประสิทธิภาพและให้ผลลัพธ์ที่เพียงพอสำหรับการแสดงผลเส้นขอบและเงา

การต่อสี

การวาดภาพที่น่าสนใจซึ่งเกิดขึ้นในเบราว์เซอร์ไม่ได้ระบุไว้ใน CSS โดยจะแสดงเส้นขอบที่มีสีหรือสไตล์ไม่สม่ำเสมอ เช่น องค์ประกอบมีเส้นขอบด้านบนสีเขียวทึบและเส้นขอบด้านขวาสีเหลืองแบบประ ในกรณีนี้ Miter คือเส้นรอยบากที่อยู่ระหว่าง มุมที่เกี่ยวข้องของขอบเส้นขอบกับมุมที่เกี่ยวข้องของขอบระยะเว้น โดยจะสร้างขอบเขตระหว่างขอบที่อยู่ติดกัน แม้ว่าจะไม่ได้ระบุไว้ แต่การแสดงผลจะค่อนข้างสอดคล้องกันระหว่างเบราว์เซอร์

การติดตั้งใช้งานใน Blink (และในเบราว์เซอร์อื่นๆ) มีดังนี้ ขอบที่กำลังจะระบายสีจะถูกตัดอย่างหยาบๆ เหมือนรูปหลายเหลี่ยมที่ตัดกัน ที่มุมแหลม โดยคำนวณในลักษณะที่จะรวมขอบที่เกี่ยวข้องแต่ ไม่รวมขอบอื่นๆ วิธีนี้จะช่วยหลีกเลี่ยงการซึม การทาสีขอบด้านใดด้านหนึ่งด้วยสไตล์และสีที่ไม่ถูกต้อง

จนถึงตอนนี้ รูปหลายเหลี่ยมนี้ค่อนข้างคำนวณได้ง่าย เนื่องจากมุมโค้งปกติ พื้นที่มุมจึงไม่เคยซ้อนทับกัน อย่างไรก็ตาม รูปทรงนี้จะเปลี่ยนไปเมื่อใช้ไฮโปเอลลิปส์และโดยเฉพาะอย่างยิ่งเมื่อใช้ซูเปอร์เอลลิปส์เว้า (ค่า superellipse เป็นลบ) ซึ่งอาจสร้างรูปร่างที่น่าสนใจได้ แต่จะทำให้รูปหลายเหลี่ยมที่เกิดจากการตัดกันแบบง่ายๆ มีแนวโน้มที่จะซ้อนทับกันและ "ล้น" ออกมา

ลองพิจารณา CSS ต่อไปนี้

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}

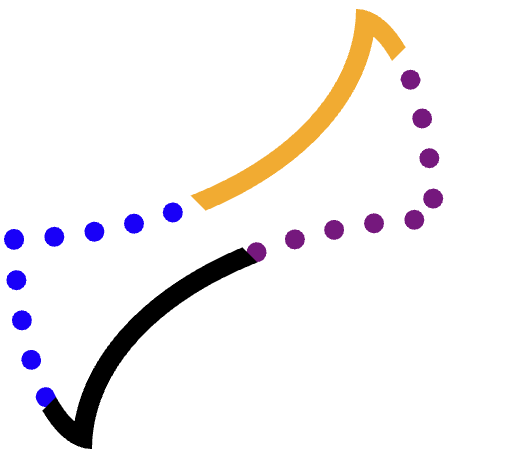
เราต้องการตัดขอบแต่ละขอบ (ส้ม จุดม่วง ดำ จุดน้ำเงิน) แยกกัน แล้ววาดเส้นทาง

หากต้องการทำเช่นนี้โดยไม่ทับซ้อนกับมุมอื่นๆ อีก 3 มุม คุณจะต้องตัดอย่างระมัดระวัง

เช่น ลองพิจารณาขอบสีส้ม (ด้านบน)

การค้นหารูปหลายเหลี่ยมที่ตรงกันซึ่งครอบคลุมขอบทั้งหมดและไม่ล้ำเข้าไปในขอบสีม่วง สีเหลือง หรือแม้แต่สีดำนั้นเป็นเรื่องยาก ส่วนรูปร่างอื่นๆ จะมีความท้าทายมากกว่า

กระบวนการนี้เกี่ยวข้องกับ 3 คลิป

คลิปแรกจะรวมขอบทั้งหมดที่มีมุมเต็ม (ไม่มีการต่อมุม) เช่น

ซึ่งประกอบด้วยมุม 2 มุม (มุมหนึ่งเป็น scoop อีกมุมหนึ่งเป็นวงกลม) โดยมีขอบขั้นต่ำเชื่อมต่อกันที่ปลาย

การเริ่มต้นจากรูปร่างนี้จะช่วยขจัดรอยซ้อนทับกับขอบตรงข้าม และตอนนี้มีเพียง 2 มุมเท่านั้นที่ยังคงเป็นปัญหา

ซึ่งทำได้โดยการตัดรูปหลายเหลี่ยมออกจากมุมนี้ ซึ่งผ่านระหว่างมุมขอบเส้นขอบและมุมขอบระยะห่าง และหยุดเมื่อกำลังจะตัดกับขอบ

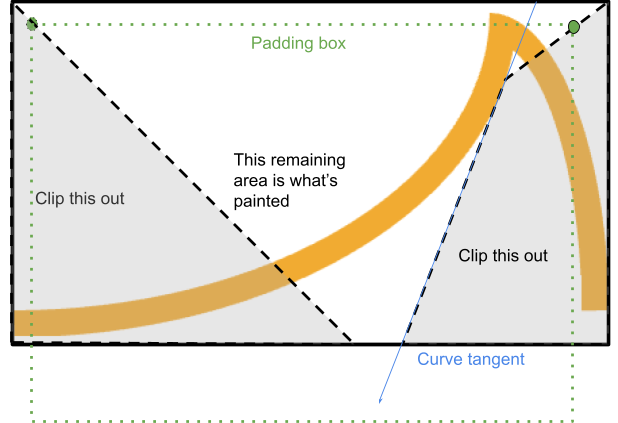
ระบบจะหาจุดที่เส้นจากขอบเส้นขอบไปยังขอบระยะห่างตัดกับเส้นสัมผัสของเส้นโค้งจากจุดเริ่มต้นที่เกี่ยวข้อง (หากเส้นโค้งเว้า)

หากจุดนั้นอยู่ภายในพื้นที่ที่แสดงผล กระบวนการจะหยุดที่จุดนั้นและดำเนินการต่อตามเส้นสัมผัสนั้นจนกว่าจะพบกล่องขอบอีกครั้ง ซึ่งจะทำให้รูปสี่เหลี่ยมสมบูรณ์

ไม่เช่นนั้นจะตัดรูปสามเหลี่ยมธรรมดาได้

สรุป

แพลตฟอร์มเว็บช่วยให้นักออกแบบและนักพัฒนาเว็บมีพลังในการแสดงออกอย่างมาก บางครั้งพร็อพเพอร์ตี้ CSS ที่ใช้ค่าตัวเลขเดียวอาจซ่อนความซับซ้อนที่สำคัญไว้เบื้องหลังเพื่อให้แสดงผลได้อย่างถูกต้องและสอดคล้องกัน

ฟีเจอร์ corner-shape มีความซับซ้อนที่น่าประหลาดใจ เอกสารนี้มีจุดมุ่งหมายเพื่อช่วยนักพัฒนาซอฟต์แวร์ในอนาคตที่ทำงานกับฟีเจอร์นี้ใน Blink, เบราว์เซอร์อื่นๆ หรือข้อกำหนด