Особенности реализации CSS corner-shape в Blink

Noam Rosenthal

Опубликовано: 19 февраля 2026 г.

Одной из функций CSS, появившихся в Chrome в 2025 году, стала corner-shape . Она позволяет задавать форму угла с border-radius с помощью ключевых слов, таких как bevel и scoop . Также можно использовать функцию superellipse , которая принимает значение от -Infinity до Infinity .

Подробный обзор этой функции и принципов её работы вы найдете в обширной статье Амита Шина на сайте Frontend Masters .

При реализации этой функции в начале 2025 года я столкнулся с несколькими интересными задачами различной сложности. Я многому научился в области суперэллипсов, рисования границ в Blink и использования векторной математики для 2D-графики.

В этом документе я делюсь некоторыми вещами, которые узнал, и которые могут быть интересны и другим.

Симметрия выпуклых и вогнутых форм

В то время как значения superellipse ( k ) традиционно находятся в диапазоне от 0 до Infinity , где значения от 0 до 1 являются вогнутыми, а остальные — выпуклыми (1 соответствует bevel ), в спецификации CSS значения superellipse находятся в диапазоне от -Infinity до Infinity и представляют собой k . Это создает симметрию, поскольку любое положительное значение выглядит как зеркальное отражение своего отрицательного аналога.

Однако по умолчанию формула superellipse работает не так.

Формула superellipse : x k + y k = 1 Обратная формула, x 1/k + y 1/k = 1 , не дает визуально симметричной кривой.

Например, при k равном 2 :

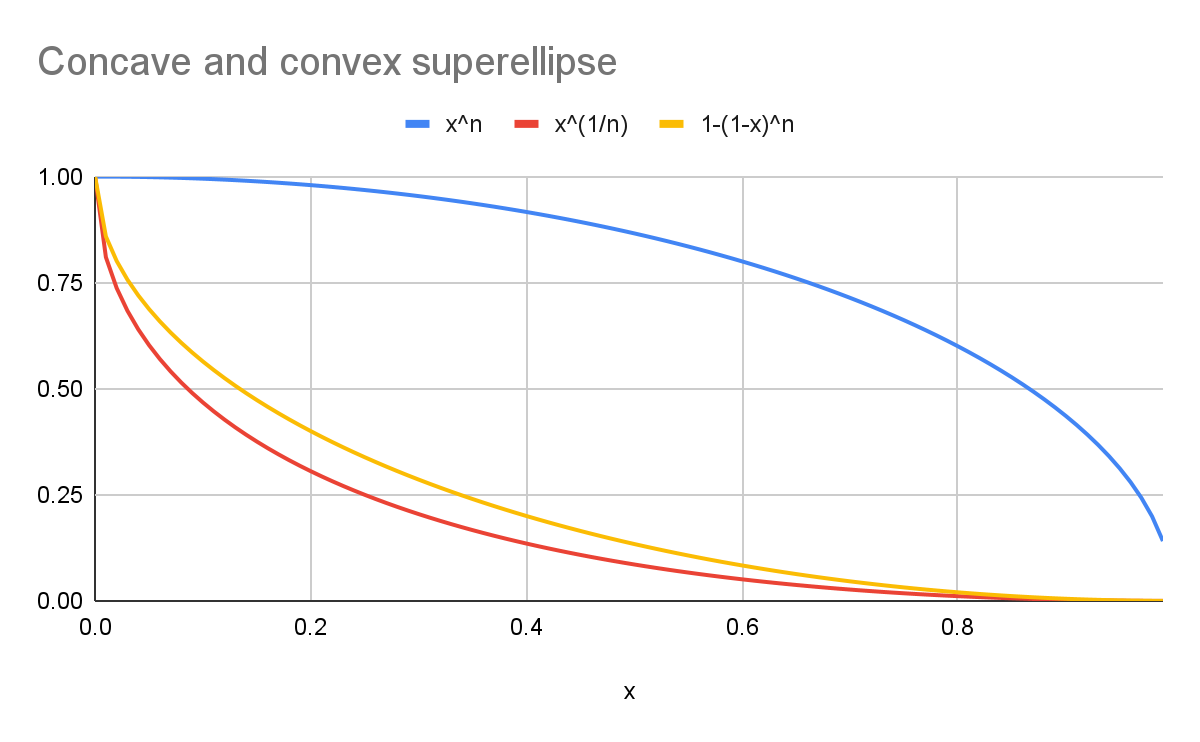
• Синяя кривая представляет собой круглый superellipse ( y=x n ).
• Красная кривая представляет собой superellipse scoop с канонической формулой ( y=x 1/n ).
• Желтая кривая представляет собой кривую, визуально симметричную синей кривой ( y=1-(1-x) n ).

Как видно из диаграммы, формы не одинаковые!

Я не буду углубляться в математические аспекты, но это связано с двойными нормами и тем, как мы воспринимаем кривизну.

С точки зрения спецификации и реализации, здесь мы представляем нечто визуальное, поэтому при вычислении вогнутых форм мы используем симметричные эквиваленты. Остальные вычисления выполняются для выпуклых форм ( k>=1 или положительных значений суперэллипса).

Формула в замкнутой форме

Следующая задача — представить кривую, или периметр superellipse , в замкнутой форме , используя формулу, состоящую из простых арифметических операций. Это крайне важно для повышения производительности, поскольку позволяет системе передавать отрисовку superellipse графическому движку.

Графические движки, такие как Skia, хорошо знакомы с кривыми Безье, поэтому представление superellipse с помощью небольшого количества кривых Безье, аппроксимирующих его периметр, делает рендеринг кривой superellipse более производительным.

К счастью, используя символическую регрессию , мы можем найти формулу, которая представляет половину выпуклого угла в виде единой кубической кривой Безье.

Кубическая кривая Безье имеет четыре точки:

• Первая точка — ( 0, 1 ).
• Последняя точка — это фактический полуугол суперэллипса: 0.5 1/k ,0.5 1/k .
• Первая контрольная точка простирается на том же уровне, что и начальная точка: ( a, 1 ).
• Вторая контрольная точка расположена по диагонали в полууглу: (0.5 1/k - b,0.5 1/k + b) .

Используемое здесь значение половины угла является очень важной координатой, которую мы будем использовать для дальнейших вычислений.

Где a и b вычисляются из k с помощью символической регрессии.

Для наглядной демонстрации посмотрите этот пример на Codepen.

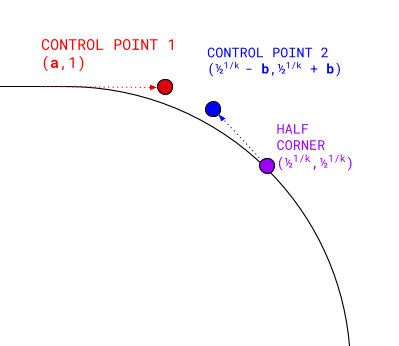
Вычисление этих четырех точек и построение кубической кривой Безье между ними дает замкнутую форму выпуклого полуугла с заданным k . Затем мы можем повернуть результаты, чтобы заполнить остальную часть угла, применить их к другим углам и перевернуть, чтобы отобразить вогнутые эквиваленты.

Не вдаваясь в математические подробности, формула для вычисления a и b выглядит следующим образом:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

Границы и тени

Помимо вычисления контура периметра угла, система также вычисляет, как он выглядит при смещении внутрь (граница или вставка box-shadow ) или наружу ( outline или обычная box-shadow ). В обычных графических библиотеках это делается с помощью обводки.

Однако границы и тени в CSS имеют характеристики отображения, отличающиеся от обводки:

• Границы неоднородны.
• Например, верхняя граница может составлять 10 пикселей, а правая — 5 пикселей, при этом угол будет интерполироваться между ними.
• Кроме того, они направлены внутрь, а не в стороны.
• Тени и контуры отображаются не совсем так, как обводка.
• Вместо этого они корректируют положение таким образом, чтобы углы выглядели острыми.

Хотя обычный путь отрисовки границы и тени хорошо работал для corner-shape (например, squircle ), и его можно повернуть на 90 градусов для форм с более вогнутыми формами, чем scoop , этот метод по умолчанию не работает для corner-shape от -1 до 1, поскольку смещение границы или тени параллельно краю приводит к тому, что угол выглядит неравномерно по ширине.

Например, если взять bevel угол и сместить границу на несколько пикселей в обе стороны, получится эффект «живота», когда середина угла выглядит шире, чем его края.

Чтобы это учесть, цель состоит в создании эффекта, работающего как обводка: найти нормаль кривой угла в начале и сделать ее длиной, равной ширине border или shadow-spread .

К счастью, это необходимо только для субэллипсов (промежуточных между bevel и закругленным), поскольку гиперэллипсы, такие как squircle работают как положено.

Для нахождения нормали субэллиптической кривой достаточно найти нормаль её квадратичной аналогии, поскольку субэллипсы и их квадратичные эквиваленты находятся близко друг к другу.

Используя ту же самую полуточку угла, вычисленную ранее, можно найти квадратичную кривую с той же средней точкой, определить ее контрольную точку, и оттуда вычисление нормали становится простым.

Нормаль продолжается с той же длиной, что и border-width или shadow-spread , а затем обрезает полученную кривую по краям (внутренний край для границы, внешний край для тени), чтобы создать непрерывный путь.

Посмотрите этот пример на CodePen.

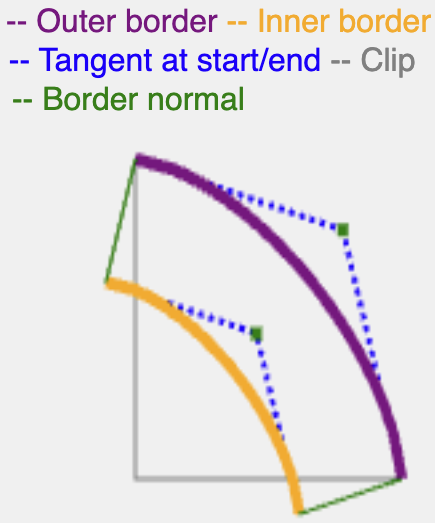
Существуют более математически точные способы вычисления касательной к superellipse , но этот метод эффективен и дает адекватные результаты для отображения границ и теней.

Цветовые соединения

Интересный приём отрисовки, который не описан в CSS, заключается в отображении границ с неравномерными цветами или стилями. Например, когда у вашего элемента верхняя граница сплошная зелёная, а правая — пунктирная жёлтая. В таких случаях линия среза проходит между соответствующим углом края границы и соответствующим углом отступа. Она создаёт границу между смежными краями. Хотя это и не указано, отображение в браузерах в целом согласуется.

В Blink (и других браузерах) это реализовано следующим образом. Край, который собирается быть отрисован, грубо обрезается, как многоугольник, пересекающийся в точке среза, вычисленный таким образом, чтобы он включал соответствующий край, но не включал другие края. Это позволяет избежать «просачивания» , то есть отрисовки одного из других краев неправильным стилем и цветом.

Вычисление этого многоугольника до сих пор было относительно простым, поскольку при наличии правильных закругленных углов области углов никогда не могут перекрываться. Однако ситуация меняется с гипоэллипсами и, в частности, с вогнутыми суперэллипсами (с отрицательными значениями superellipse ). Они могут создавать довольно интересные формы, из-за которых простые многоугольники пересечения очень склонны к перекрытиям и «расхождению».

Рассмотрим следующий CSS-код:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}

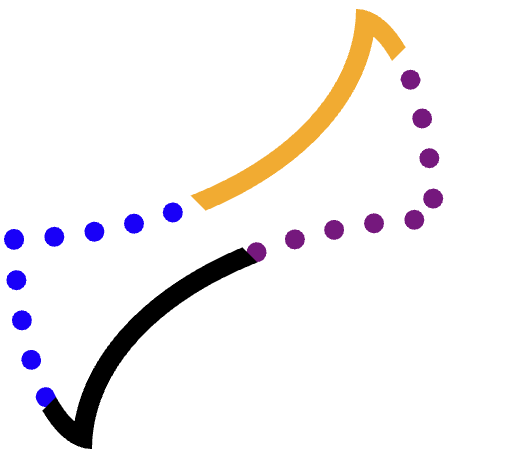
Мы хотим обрезать каждый край (оранжевый, фиолетовый пунктирный, черный, синий пунктирный) отдельно, а затем нарисовать контур.

Для достижения этого без наложения на три других угла необходима аккуратная обрезка.

Например, рассмотрим оранжевый (верхний) край.

Трудно найти такой многоугольник, который бы точно включал всю эту грань и не выходил за её пределы, затрагивая фиолетовые, жёлтые или даже чёрные края. С некоторыми другими фигурами задача сложнее.

Этот процесс включает в себя три зажима.

Первый фрагмент охватывает весь край, включая весь угол (без косого среза). Например:

Она состоит из двух углов (одного scoop и одного закругления), между которыми имеется минимальный выступ, соединенных на концах.

Исходя из такой формы, исключаются наложения с противоположным краем, и теперь остаются только два косых среза.

Это достигается путем отсечения от этого угла многоугольника, проходящего между углами границы и отступа, и останавливающегося в момент, когда он вот-вот пересечется с краем:

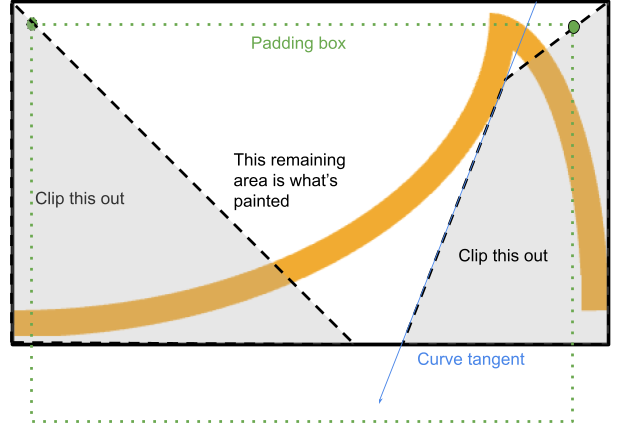
Система находит точку пересечения линии, проведенной от края границы к краю отступа, с касательной к кривой, проведенной из соответствующей начальной точки (если кривая вогнутая).

Если эта точка находится внутри области отрисовки, процесс останавливается там и продолжается вдоль касательной до тех пор, пока она снова не встретится с граничным прямоугольником, завершая формирование четырехугольника.

В противном случае, можно обрезать простой треугольник.

Краткое содержание

Веб-платформа предоставляет веб-дизайнерам и разработчикам значительные возможности для самовыражения. Иногда свойство CSS, принимающее одно числовое значение, скрывает под собой значительную сложность, необходимую для точного и согласованного отображения.

Функция corner-shape оказалась на удивление сложной. Данная документация призвана помочь будущим разработчикам, работающим над этой функцией в Blink, других браузерах или в соответствии со спецификацией.