Publié le : 19 février 2026
L'une des fonctionnalités CSS que Chrome a déployées en 2025 était corner-shape.
Cela vous permet de définir la forme d'un angle qui comporte un border-radius à l'aide de mots clés tels que bevel et scoop. Vous pouvez également utiliser une fonction superellipse qui reçoit une valeur comprise entre -Infinity et Infinity.
Pour obtenir une présentation détaillée de la fonctionnalité et de son fonctionnement, consultez le long article d'Amit Sheen sur Frontend Masters.
Lors de l'implémentation de cette fonctionnalité au début de l'année 2025, j'ai rencontré quelques défis intéressants de complexité variable. J'ai beaucoup appris sur les superellipses, la peinture de bordures dans Blink et l'utilisation des mathématiques vectorielles pour les graphiques 2D.
Ce document partage certaines des choses que j'ai apprises, qui pourraient également intéresser d'autres personnes.
Symétrie des formes convexes et concaves
Alors que les valeurs superellipse (k) sont traditionnellement comprises entre 0 et Infinity, où les valeurs comprises entre 0 et 1 sont concaves et les autres sont convexes (1 étant bevel), les valeurs superellipse de la spécification CSS sont comprises entre -Infinity et Infinity, et représentent 2k. Cela crée une symétrie, car toute valeur positive ressemble à l'image miroir de sa contrepartie négative.
Toutefois, par défaut, la formule superellipse ne fonctionne pas de cette manière.
La formule superellipse est la suivante : xk + yk = 1. La formule inverse, x1/k + y1/k = 1, ne produit pas de courbe visuellement symétrique.
Par exemple, avec un k de 2 :
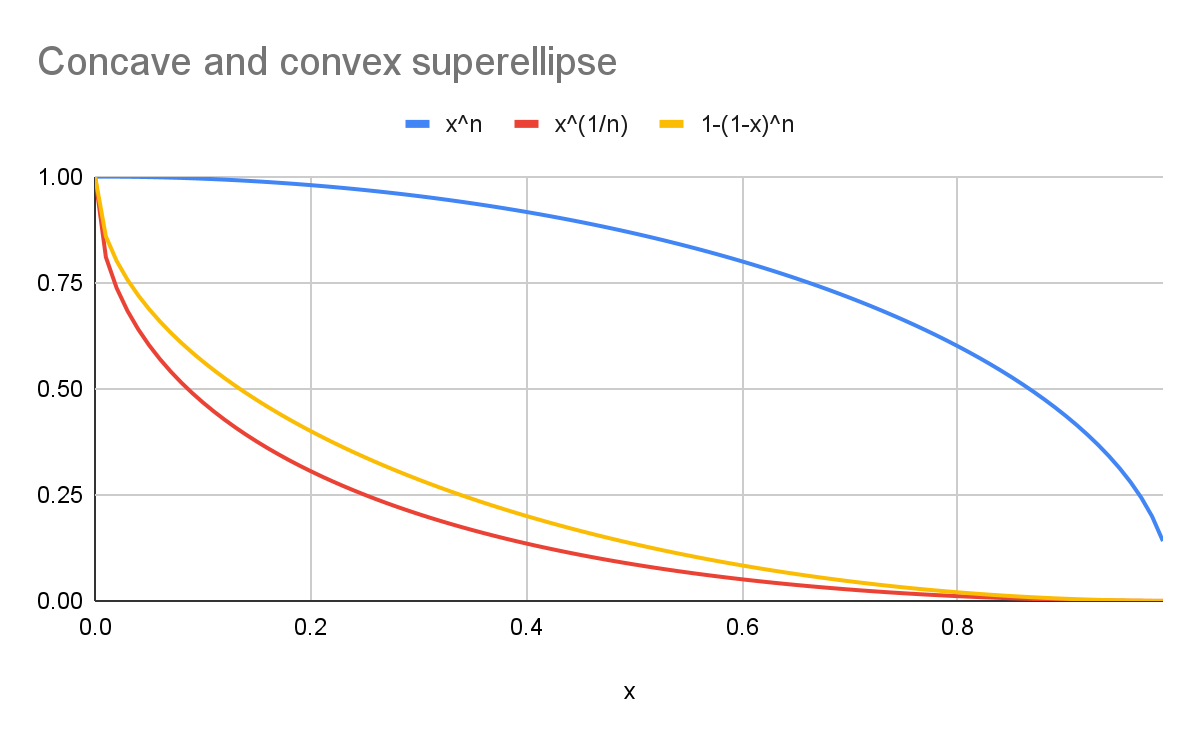
- La courbe bleue représente un tour
superellipse(y=xn). - La courbe rouge représente une
scoopsuperellipseavec la formule canonique (y=x1/n). - La courbe jaune représente une courbe visuellement symétrique à la courbe bleue (
y=1-(1-x)n).
Comme le montre le graphique, les formes ne sont pas identiques.
Je ne vais pas entrer dans les détails mathématiques, mais cela a à voir avec les normes doubles et la façon dont nous percevons la courbure.
En termes de spécification et d'implémentation, nous représentons ici quelque chose de visuel. Nous utilisons donc les équivalents symétriques lors du calcul des formes concaves. Le reste des calculs mathématiques est effectué sur des formes convexes (k>=1 ou valeurs de superellipse positives).
Formule de forme fermée
Le prochain défi consiste à représenter la courbe, ou le périmètre de superellipse, sous forme fermée, c'est-à-dire une formule composée d'opérations arithmétiques simples.
C'est essentiel pour les performances, car cela permet au système de confier le rendu superellipse au moteur graphique.
Les moteurs graphiques tels que Skia connaissent bien les courbes de Bézier. Par conséquent, représenter un superellipse avec un petit nombre de courbes de Bézier qui approximeront son périmètre rendra le rendu d'une courbe superellipse plus performant.
Heureusement, grâce à la régression symbolique, nous pouvons trouver une formule qui représente la moitié d'un angle convexe sous la forme d'une seule courbe de Bézier cubique.
Une courbe de Bézier cubique comporte quatre points :
- Le premier point est (
0, 1). - Le dernier point est le demi-coin de la superellipse :
0.51/k,0.51/k. - Le premier point de contrôle s'étire au même niveau que le point de départ : (
a, 1). - Le deuxième point de contrôle est en diagonale de la demi-extrémité :
(0.51/k - b,0.51/k + b).
La valeur de demi-angle utilisée ici est une coordonnée très importante que nous allons utiliser pour d'autres calculs par la suite.
Où a et b sont calculés à partir de k à l'aide de la régression symbolique.
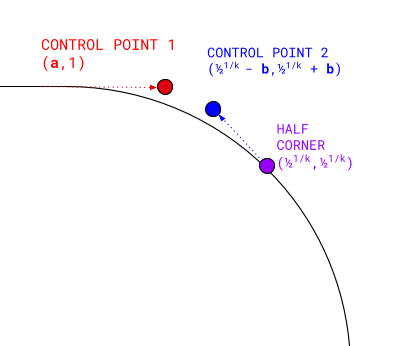
Le calcul de ces quatre points et le rendu d'une courbe de Bézier cubique entre eux fournissent un demi-coin convexe de forme fermée avec un k donné. Nous pouvons ensuite faire pivoter les résultats pour remplir le reste de l'angle, les appliquer aux autres angles et les inverser pour obtenir les équivalents concaves.
Sans entrer plus en détail dans les mathématiques, voici la formule permettant de calculer a et b :
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Bordures et ombres
En plus de calculer le chemin du périmètre de l'angle, le système calcule également son apparence lorsqu'il est décalé vers l'intérieur (une bordure ou un box-shadow en retrait) ou vers l'extérieur (un outline ou un box-shadow normal). Dans les bibliothèques graphiques classiques, cela se fait par tracé.
Toutefois, les bordures et les ombres en CSS présentent des caractéristiques de rendu différentes de celles des traits :
- Les bordures ne sont pas uniformes.
- Par exemple, la bordure supérieure peut être de 10 pixels et la bordure de droite de 5 pixels, avec l'angle interpolant entre les deux.
- De plus, ils sont orientés vers l'intérieur plutôt que vers les deux côtés.
- Les ombres et les contours ne sont pas rendus exactement comme un trait.
- Au lieu de cela, ils s'ajustent pour que les angles soient nets.
Bien que le chemin de rendu habituel des bordures et des ombres fonctionne bien pour les valeurs corner-shape arrondies ou plus convexes (par exemple, squircle), et qu'il puisse être pivoté de 90 degrés pour les formes plus concaves qu'un scoop, cette valeur par défaut ne fonctionne pas pour les valeurs corner-shape comprises entre -1 et 1. En effet, le décalage de la bordure ou de l'ombre parallèlement au bord produit un angle qui semble avoir une largeur inégale.
Par exemple, si vous prenez un angle bevel et que vous décallez la bordure de quelques pixels de chaque côté, vous créez un effet de "ventre", où le milieu de l'angle semble plus large que les côtés.
Pour tenir compte de cela, l'objectif est de créer un effet qui fonctionne comme un trait : trouver la normale de la courbe d'angle au début et la rendre aussi longue que la largeur de border ou shadow-spread.
Heureusement, cela n'est nécessaire que pour les sous-ellipses (entre bevel et rond), car les hyper-ellipses comme squircle fonctionnent comme prévu.
Pour trouver la normale d'une courbe de sous-ellipse, il suffit de trouver la normale de sa courbe quadratique équivalente, car les sous-ellipses et leurs équivalents de courbe quadratique sont proches les uns des autres.
En utilisant le même demi-angle calculé précédemment, vous pouvez trouver une courbe quadratique qui a le même point central, dériver son point de contrôle quadratique, et à partir de là, calculer la normale est simple.
La normale se poursuit avec la même longueur que border-width ou shadow-spread, puis découpe la courbe résultante avec les bords (bord intérieur pour la bordure, bord extérieur pour l'ombre) afin de créer un chemin continu.
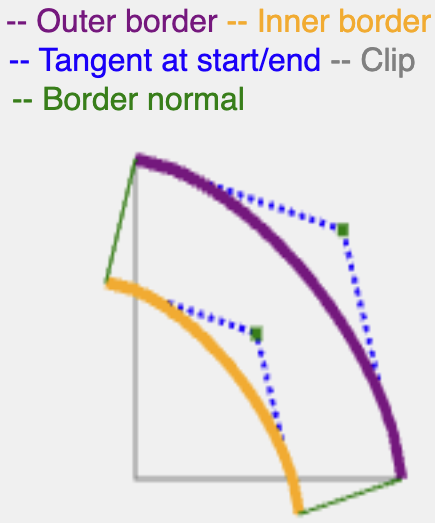
Il existe des méthodes plus précises mathématiquement pour calculer une tangente pour un superellipse, mais celle-ci est efficace et produit des résultats adéquats pour le rendu des bordures et des ombres.
Joindre les couleurs
Une partie intéressante de la peinture qui se produit dans les navigateurs n'est pas spécifiée dans CSS. Il affiche les bordures dont les couleurs ou les styles ne sont pas uniformes. Par exemple, si votre élément a une bordure supérieure verte et pleine, et une bordure droite jaune et en pointillés. Dans ce cas, le biseau est une ligne d'incision qui se situe entre l'angle correspondant de la bordure et l'angle correspondant de la marge intérieure. Elle crée la limite entre les bords adjacents.Bien que non spécifiée, le rendu est assez cohérent entre les navigateurs.
Voici comment cela est implémenté dans Blink (et dans d'autres navigateurs). Le bord qui est sur le point d'être peint est grossièrement coupé comme un polygone qui se croise au niveau de la mitre, calculé de manière à inclure le bord concerné, mais pas les autres bords. Cela évite le débordement, qui consiste à peindre l'un des autres bords avec un style et une couleur incorrects.
Jusqu'à présent, ce polygone était relativement simple à calculer, car avec des coins arrondis réguliers, les zones d'angle ne peuvent jamais se chevaucher. Toutefois, cela change avec les hypo-ellipses et plus précisément avec les superellipses concaves (valeurs superellipse négatives). Elles peuvent créer des formes assez intéressantes qui rendent les polygones d'intersection naïfs très sujets aux chevauchements et aux "fuites".
Prenons l'exemple du code CSS suivant :
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
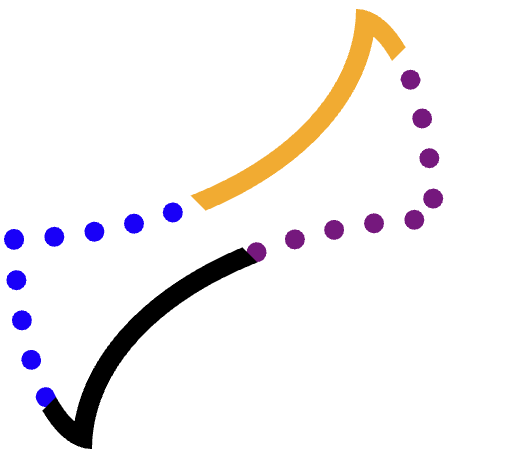
Nous voulons découper chaque bord (orange, violet pointillé, noir, bleu pointillé) séparément, puis dessiner le chemin.
Pour ce faire sans chevaucher aucun des trois autres angles, un découpage précis est nécessaire.
Par exemple, prenons le bord orange (en haut).
Il est difficile de trouver un polygone exact qui inclut l'intégralité de cette bordure sans empiéter sur les bordures violettes, jaunes ou même noires. D'autres formes sont plus difficiles à réaliser.
Ce processus implique trois extraits.
Le premier clip inclut l'intégralité de la bordure, avec l'angle complet (sans onglet). Exemple :

Il se compose de deux angles (un scoop et un arrondi), avec un bord minimal entre eux, reliés aux extrémités.
En commençant par cette forme, vous éliminez les chevauchements avec le bord opposé. Seuls les deux onglets restent un problème.
Pour ce faire, un polygone est découpé à partir de ce coin. Il passe entre les coins de la bordure et de la marge intérieure, et s'arrête au moment où il est sur le point d'intersecter le bord :
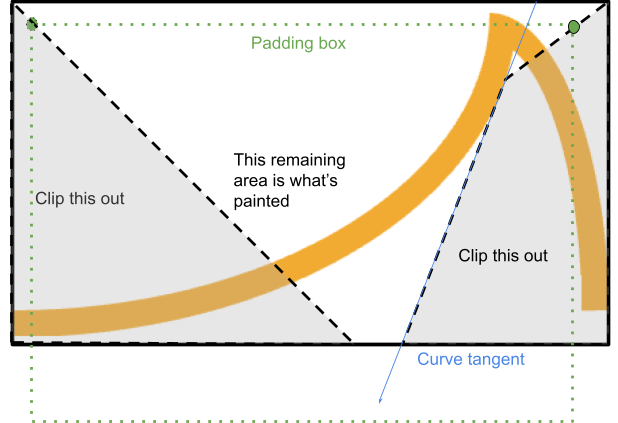
Le système trouve le point où une ligne allant du bord de la bordure au bord de la marge intérieure croise la tangente de la courbe à partir du point de départ concerné (si la courbe est concave).
Si ce point se trouve dans la zone rendue, le processus s'arrête là et se poursuit le long de cette tangente jusqu'à ce qu'il rencontre à nouveau la boîte de bordure, ce qui complète un quad.
Sinon, un simple triangle peut être découpé.
Résumé
La plate-forme Web offre aux concepteurs et développeurs Web une grande puissance d'expression. Parfois, une propriété CSS qui prend une seule valeur numérique cache une complexité importante en coulisses pour qu'elle s'affiche de manière précise et cohérente.
La fonctionnalité corner-shape s'est avérée étonnamment complexe. Cette documentation vise à aider les futurs développeurs qui travailleront sur cette fonctionnalité dans Blink, d'autres navigateurs ou la spécification.

