Xuất bản: Ngày 19 tháng 2 năm 2026
Một trong những tính năng CSS mà Chrome phát hành vào năm 2025 là corner-shape.
Thao tác này cho phép bạn xác định hình dạng của một góc có border-radius bằng cách sử dụng các từ khoá như bevel và scoop. Bạn cũng có thể sử dụng hàm superellipse nhận giá trị trong khoảng từ -Infinity đến Infinity.
Hãy xem bài viết chi tiết của Amit Sheen tại Frontend Masters để biết thông tin tổng quan về tính năng này và cách hoạt động của tính năng này.
Khi triển khai tính năng này vào đầu năm 2025, tôi đã gặp phải một số thách thức thú vị với độ phức tạp khác nhau. Tôi đã học được rất nhiều về siêu elip, vẽ đường viền trong Blink và sử dụng toán học vectơ cho đồ hoạ 2D.
Tài liệu này chia sẻ một số điều tôi học được, có thể cũng thú vị đối với những người khác.
Tính đối xứng của hình lồi và hình lõm
Mặc dù các giá trị superellipse (k) thường nằm trong khoảng từ 0 đến Infinity, trong đó các giá trị từ 0 đến 1 là lõm và các giá trị còn lại là lồi (1 là bevel), các giá trị superellipse trong quy cách CSS nằm trong khoảng từ -Infinity đến Infinity và biểu thị 2k. Điều này tạo ra sự đối xứng vì mọi giá trị dương đều trông giống như hình ảnh phản chiếu của giá trị âm tương ứng.
Tuy nhiên, theo mặc định, công thức superellipse không hoạt động theo cách đó.
Công thức superellipse là: xk + yk = 1. Công thức nghịch đảo x1/k + y1/k = 1 không tạo ra đường cong đối xứng trực quan.
Ví dụ: với k là 2:
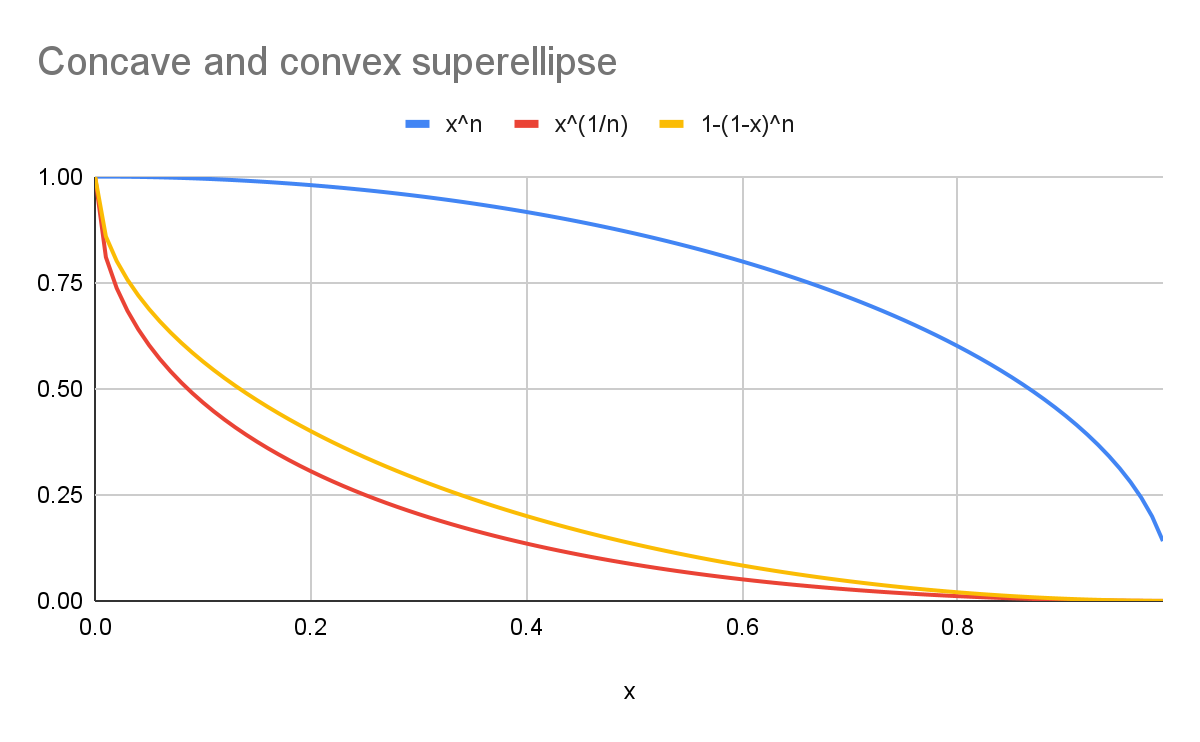
- Đường cong màu xanh dương biểu thị một vòng
superellipse(y=xn). - Đường cong màu đỏ biểu thị một
scoopsuperellipsevới công thức chính tắc (y=x1/n). - Đường cong màu vàng biểu thị một đường cong đối xứng trực quan với đường cong màu xanh dương (
y=1-(1-x)n).
Như biểu đồ cho thấy, các hình dạng này không giống nhau!
Tôi sẽ không đi sâu vào toán học của vấn đề này, nhưng nó liên quan đến các chuẩn kép và cách chúng ta cảm nhận độ cong.
Về quy cách và cách triển khai, chúng ta đang biểu thị một thứ gì đó trực quan ở đây, vì vậy, chúng ta sử dụng các giá trị tương đương đối xứng khi tính toán các hình dạng lõm. Phần còn lại của phép toán được thực hiện trên các hình dạng lồi (k>=1 hoặc các giá trị siêu elip dương).
Công thức dạng đóng
Thử thách tiếp theo là biểu diễn đường cong hoặc chu vi của superellipse ở dạng khép kín, một công thức được tạo thành từ các phép tính số học đơn giản.
Điều này là cần thiết cho hiệu suất, cho phép hệ thống chuyển quá trình kết xuất superellipse sang công cụ đồ hoạ.
Các công cụ đồ hoạ như Skia quen thuộc với đường cong Bezier, vì vậy, việc biểu thị một superellipse bằng một số ít đường cong Bezier xấp xỉ chu vi của đường cong đó sẽ giúp kết xuất đường cong superellipse hiệu quả hơn.
May mắn thay, bằng cách sử dụng hồi quy tượng trưng, chúng ta có thể tìm ra một công thức biểu thị một nửa góc lồi dưới dạng một đường cong Bezier bậc ba duy nhất.
Đường cong Bezier bậc ba có 4 điểm:
- Điểm đầu tiên là (
0, 1). - Điểm cuối cùng là nửa góc siêu elip thực tế:
0.51/k,0.51/k. - Điểm kiểm soát đầu tiên kéo dài ở cùng cấp với điểm bắt đầu: (
a, 1). - Điểm kiểm soát thứ hai là đường chéo của nửa góc:
(0.51/k - b,0.51/k + b).
Giá trị nửa góc được dùng ở đây là một toạ độ rất quan trọng mà chúng ta sẽ dùng cho các phép tính khác sau này.
Trong đó, a và b được tính toán từ k bằng cách sử dụng hồi quy tượng trưng.
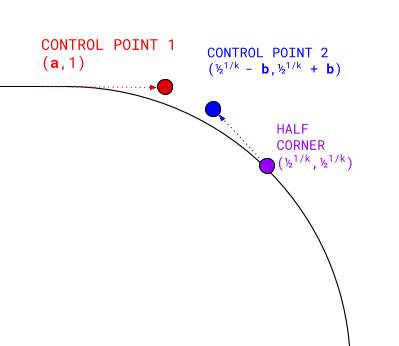
Việc tính toán 4 điểm này và kết xuất đường cong Bezier bậc ba giữa chúng sẽ tạo ra một nửa góc lồi dạng khép kín với k cho trước. Sau đó, chúng ta có thể xoay các kết quả để lấp đầy phần còn lại của góc, áp dụng cho các góc khác và lật chúng để hiển thị các kết quả tương đương dạng lõm.
Không cần đi sâu vào các chi tiết toán học, công thức để tính a và b là:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Đường viền và bóng
Ngoài việc tính toán đường viền của góc, hệ thống cũng tính toán cách đường viền xuất hiện khi được bù vào trong (đường viền hoặc box-shadow lồng) hoặc ra ngoài (outline hoặc box-shadow thông thường). Trong các thư viện đồ hoạ thông thường, việc này được thực hiện bằng cách vẽ đường viền.
Tuy nhiên, đường viền và bóng trong CSS có các đặc điểm kết xuất khác với nét vẽ:
- Đường viền không đồng nhất.
- Ví dụ: đường viền trên cùng có thể là 10 pixel và đường viền bên phải là 5 pixel, với góc nội suy giữa chúng.
- Ngoài ra, các đường này hướng vào trong thay vì hướng ra cả hai bên.
- Đổ bóng và đường viền không kết xuất chính xác như một nét vẽ.
- Thay vào đó, chúng sẽ điều chỉnh để các góc xuất hiện sắc nét.
Mặc dù đường dẫn kết xuất bóng và đường viền thông thường hoạt động tốt cho các giá trị corner-shape có dạng tròn hoặc lồi hơn (ví dụ: squircle) và có thể xoay 90 độ cho các hình dạng lõm hơn scoop, nhưng giá trị mặc định này không hoạt động cho các giá trị corner-shape trong khoảng từ -1 đến 1, vì việc bù đường viền hoặc bóng song song với cạnh sẽ tạo ra một góc có vẻ như có chiều rộng không đồng đều.
Ví dụ: lấy một góc bevel và bù đường viền bằng một số pixel ở cả hai bên sẽ tạo ra hiệu ứng "bụng", trong đó phần giữa của góc trông rộng hơn các cạnh.
Để giải thích điều đó, mục tiêu là tạo ra một hiệu ứng hoạt động như một nét vẽ – tìm đường pháp tuyến của đường cong góc ở điểm bắt đầu và tạo đường pháp tuyến đó dài bằng chiều rộng của border hoặc shadow-spread.
May mắn thay, điều này chỉ cần thiết cho các hình bán elip (giữa bevel và hình tròn), vì các hình siêu elip như squircle hoạt động như mong đợi.
Để tìm đường pháp tuyến của một đường cong bán elip, bạn chỉ cần tìm đường pháp tuyến của đường cong bậc hai tương ứng, vì các bán elip và đường cong bậc hai tương đương của chúng gần nhau.
Bằng cách sử dụng cùng một nửa góc được tính toán trước đó, bạn có thể tìm thấy một đường cong bậc hai có cùng điểm giữa, suy ra điểm kiểm soát bậc hai và từ đó tính toán đường pháp tuyến một cách đơn giản.
Đường pháp tuyến tiếp tục với cùng độ dài như border-width hoặc shadow-spread, sau đó cắt đường cong kết quả bằng các cạnh (cạnh trong cho đường viền, cạnh ngoài cho bóng) để tạo một đường dẫn liên tục.
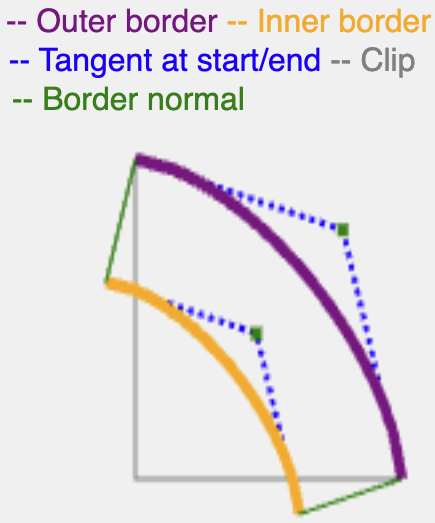
Có nhiều cách chính xác hơn về mặt toán học để tính toán đường tiếp tuyến cho một superellipse, nhưng phương pháp này hiệu quả và tạo ra kết quả phù hợp để kết xuất đường viền và bóng.
Màu nối
Một phần thú vị của quá trình kết xuất xảy ra trong trình duyệt lại không được chỉ định trong CSS. Thành phần này hiển thị các đường viền có màu sắc hoặc kiểu không đồng nhất. Ví dụ: nơi phần tử của bạn có đường viền trên liền nét màu xanh lục và đường viền phải nét đứt màu vàng. Trong những trường hợp này, đường vát là một đường cắt nằm giữa góc liên quan của cạnh viền và góc liên quan của cạnh khoảng đệm. Nó tạo ra ranh giới giữa các cạnh liền kề.Mặc dù không được chỉ định, nhưng quá trình kết xuất tương đối nhất quán giữa các trình duyệt.
Cách triển khai việc này trong Blink (và trong các trình duyệt khác) như sau. Cạnh sắp được vẽ sẽ bị cắt thô như một đa giác giao nhau tại góc nhọn, được tính toán theo cách sao cho cạnh đó sẽ bao gồm cạnh có liên quan nhưng không bao gồm bất kỳ cạnh nào khác. Điều này giúp tránh hiện tượng tràn màu, vẽ một trong các cạnh khác bằng kiểu và màu không chính xác.
Cho đến nay, đa giác này tương đối dễ tính toán, vì với các góc bo tròn thông thường, các vùng góc không bao giờ có thể chồng lên nhau. Tuy nhiên, điều này thay đổi với các đường cong gần elip và đặc biệt là với các siêu elip lõm (giá trị superellipse âm). Những đường này có thể tạo ra các hình dạng khá thú vị khiến các đa giác giao nhau đơn giản rất dễ bị chồng chéo và "tràn".
Hãy xem xét CSS sau:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
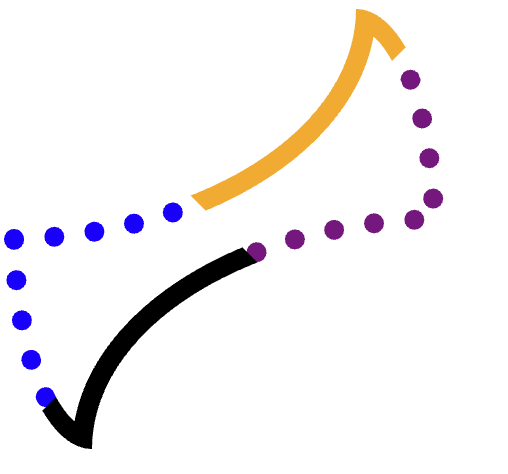
Chúng ta muốn cắt riêng từng cạnh (cam, chấm tím, đen, chấm xanh dương), sau đó vẽ đường dẫn.
Để đạt được điều này mà không bị chồng lên bất kỳ góc nào trong số 3 góc còn lại, bạn cần phải cắt cẩn thận.
Ví dụ: hãy xem xét cạnh màu cam (trên cùng).
Rất khó để tìm thấy một đa giác chính xác bao gồm toàn bộ cạnh đó và không tràn vào các cạnh màu tím, vàng hoặc thậm chí là màu đen. Một số hình dạng khác sẽ khó hơn.
Quy trình này bao gồm 3 đoạn video.
Đoạn trích đầu tiên bao gồm toàn bộ cạnh, với góc đầy đủ (không có góc vát). Ví dụ:

Hình này bao gồm 2 góc (một góc scoop, một góc tròn), với cạnh tối thiểu giữa chúng, được kết nối ở các đầu.
Bắt đầu từ hình dạng này sẽ loại bỏ các phần chồng chéo với cạnh đối diện và giờ đây, chỉ còn hai góc nhọn là vấn đề cần quan tâm.
Điều này đạt được bằng cách cắt ra từ góc này, một đa giác đi qua giữa các góc border-edge và padding-edge, đồng thời dừng lại tại thời điểm sắp giao với cạnh:
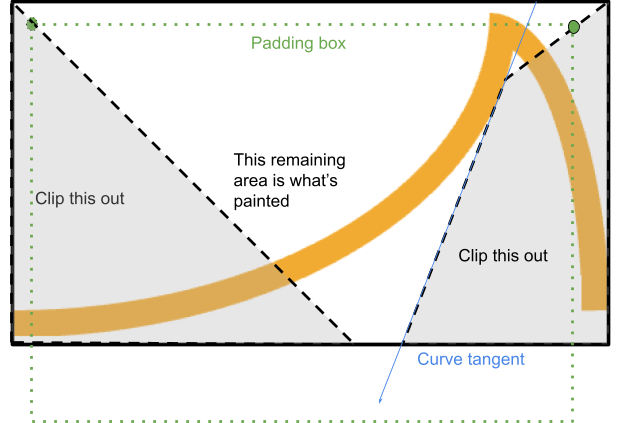
Hệ thống tìm thấy điểm mà đường thẳng từ cạnh đường viền đến cạnh khoảng đệm giao với đường tiếp tuyến của đường cong từ điểm bắt đầu có liên quan (nếu đường cong là đường cong lõm).
Nếu điểm đó nằm trong vùng được kết xuất, quy trình sẽ dừng ở đó và tiếp tục dọc theo đường tiếp tuyến đó cho đến khi gặp lại hộp đường viền, hoàn thành một tứ giác.
Nếu không, một tam giác đơn giản có thể bị cắt.
Tóm tắt
Nền tảng web mang đến cho nhà thiết kế và nhà phát triển web khả năng biểu đạt đáng kể. Đôi khi, một thuộc tính CSS nhận một giá trị số duy nhất sẽ che giấu sự phức tạp đáng kể bên dưới để hiển thị chính xác và nhất quán.
Tính năng corner-shape có độ phức tạp đáng ngạc nhiên. Tài liệu này nhằm mục đích trợ giúp những nhà phát triển trong tương lai làm việc trên tính năng này, trong Blink, các trình duyệt khác hoặc quy cách.

