Blink'te CSS köşe şekli uygulama ile ilgili uç örnekler

Noam Rosenthal

Yayınlanma tarihi: 19 Şubat 2026

Chrome'un 2025'te kullanıma sunduğu CSS özelliklerinden biri corner-shape oldu. Bu özellik, border-radius olan bir köşenin şeklini bevel ve scoop gibi anahtar kelimelerle tanımlamanıza olanak tanır. -Infinity ile Infinity arasında bir değer alan superellipse işlevini de kullanabilirsiniz.

Özelliğe ve işleyiş şekline dair harika bir genel bakış için Amit Sheen'in Frontend Masters'daki kapsamlı makalesine göz atın.

2025'in başlarında bu özelliği uygularken farklı karmaşıklık düzeylerinde birkaç ilginç zorlukla karşılaştım. Süperelipsler, Blink'te kenarlık boyama ve 2D grafikler için vektör matematiği kullanma hakkında çok şey öğrendim.

Bu belgede, öğrendiğim ve başkalarının da ilgisini çekebilecek bazı bilgileri paylaşıyorum.

Dışbükey ve içbükey şekillerin simetrisi

Geleneksel olarak superellipse (k) değerleri 0 ile Infinity arasında değişir. 0 ile 1 arasındaki değerler içbükey, diğerleri ise dışbükeydir (1, bevel'ü temsil eder). CSS spesifikasyonundaki superellipse değerleri -Infinity ile Infinity arasında değişir ve 2k'yi temsil eder. Bu sayede, pozitif değerler negatif değerlerin ayna görüntüsü gibi göründüğünden simetri oluşur.

Ancak varsayılan olarak superellipse formülü bu şekilde çalışmaz.

superellipse formülü: xk + yk = 1. Ters formül olan x1/k + y1/k = 1, görsel olarak simetrik bir eğri oluşturmaz.

Örneğin, k değeri 2 olan bir durumda:

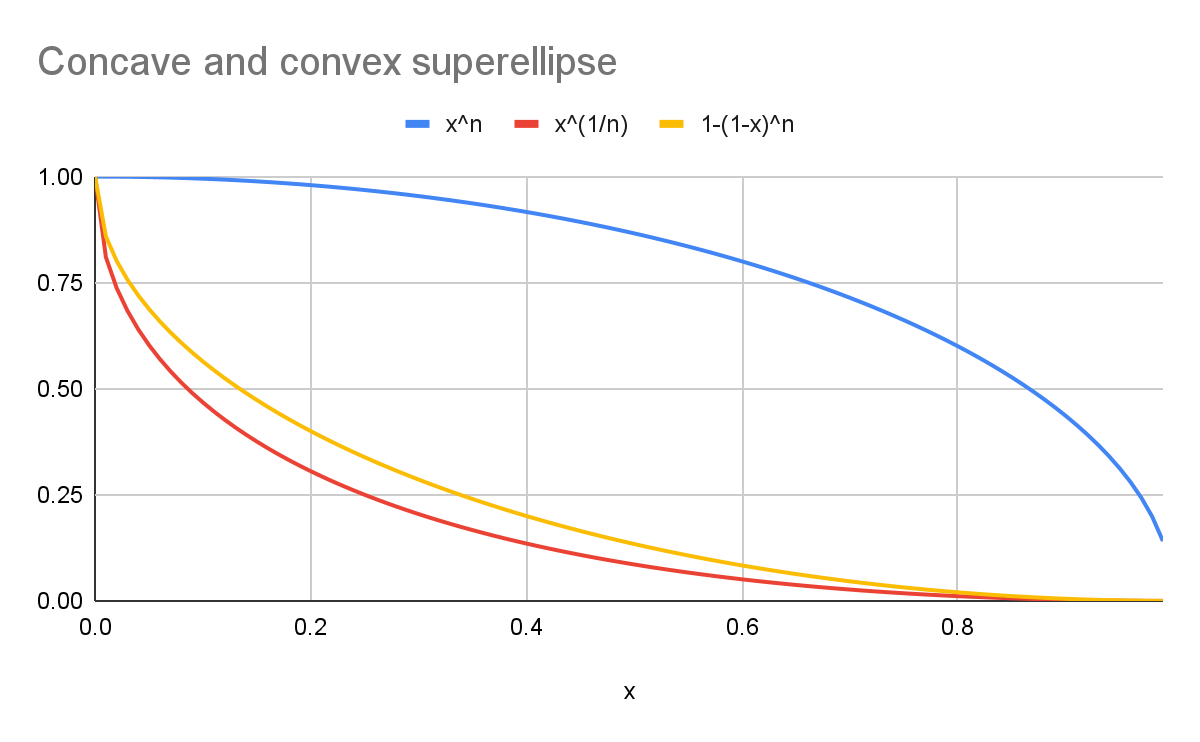
Yuvarlak bir süperelips (mavi), standart formüllü bir süperelips (kırmızı) ve görsel olarak simetrik bir eğri (sarı) gösteren süperelips eğrilerinin karşılaştırması.
  • Mavi eğri, yuvarlamayı superellipse (y=xn) temsil eder.
  • Kırmızı eğri, standart formülü (y=x1/n) olan bir scoop superellipse'yi temsil eder.
  • Sarı eğri, mavi eğriye (y=1-(1-x)n) görsel olarak simetrik olan bir eğriyi temsil eder.

Grafikte de görüldüğü gibi şekiller aynı değil.

Bunun matematiksel yönüne daha fazla değinmeyeceğim ancak bu durum, çift normlar ve eğriliği algılama şeklimizle ilgilidir.

Spesifikasyon ve uygulama açısından burada görsel bir şey gösteriyoruz. Bu nedenle, içbükey şekilleri hesaplarken simetrik eşdeğerleri kullanıyoruz. Matematiksel işlemlerin geri kalanı dışbükey şekiller (k>=1 veya pozitif süperelips değerleri) üzerinde yapılır.

Kapalı form formülü

Bir sonraki zorluk, superellipse eğrisini veya çevresini kapalı biçimde (basit aritmetik işlemlerden oluşan bir formül) ifade etmektir. Bu, sistemin superellipse oluşturma işlemini grafik motoruna devretmesini sağlayan performans için gereklidir.

Skia gibi grafik motorları Bezier eğrilerini iyi bilir. Bu nedenle, superellipse şeklini çevresini yaklaşık olarak temsil eden az sayıda Bezier eğrisiyle göstermek, superellipse eğrisinin daha iyi performansla oluşturulmasını sağlar.

Neyse ki sembolik regresyon kullanarak dışbükey bir köşenin yarısını tek bir kübik Bezier eğrisi olarak temsil eden bir formül bulabiliriz.

Kübik Bezier eğrisinin dört noktası vardır:

  • İlk nokta (0, 1).
  • Son nokta, gerçek süperelips yarı köşesidir: 0.51/k,0.51/k.
  • İlk kontrol noktası, başlangıç noktasıyla aynı seviyede içeri doğru uzanır: (a, 1).
  • İkinci kontrol noktası, yarım köşenin çaprazıdır: (0.51/k - b,0.51/k + b).

Burada kullanılan yarım köşe değeri, ileride diğer hesaplamalar için kullanacağımız çok önemli bir koordinattır.

Burada a ve b, sembolik regresyon kullanılarak k değerinden hesaplanır.

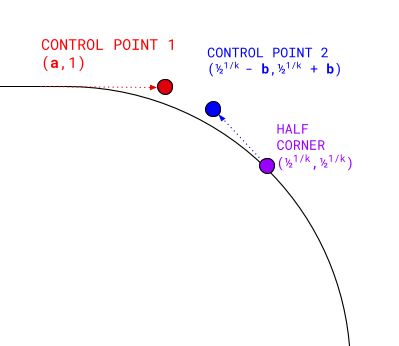
Bir eğriye eşlenmiş kontrol noktalarının resmi.
Gösterim için bu Codepen'e göz atın.

Bu dört noktayı hesaplayıp aralarında kübik Bezier eğrisi oluşturmak, belirli bir k ile kapalı biçimli dışbükey yarım köşe sağlar. Ardından, köşenin geri kalanını doldurmak için sonuçları döndürebilir, diğer köşelere uygulayabilir ve içbükey eşdeğerlerini oluşturmak için ters çevirebiliriz.

Matematiksel ayrıntılara girmeden a ve b değerlerini hesaplama formülü şöyledir:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

Kenarlıklar ve gölgeler

Köşenin çevresinin yolunu hesaplamanın yanı sıra sistem, içe (kenarlık veya girinti box-shadow) ya da dışa (outline veya normal box-shadow) doğru kaydırıldığında nasıl göründüğünü de hesaplar. Geleneksel grafik kitaplıklarında bu işlem, kontur oluşturularak yapılır.

Ancak CSS'deki kenarlıklar ve gölgeler, konturdan farklı oluşturma özelliklerine sahiptir:

  • Kenarlıklar düzgün değil.
  • Örneğin, üst kenarlık 10 piksel, sağ kenarlık ise 5 piksel olabilir. Köşe, bu iki değer arasında enterpolasyon yapar.
  • Ayrıca, bu çizgiler iki tarafa doğru değil, içe doğru gider.
  • Gölgeler ve ana hatlar, kontur gibi oluşturulmaz.
  • Bunun yerine, köşeler keskin görünecek şekilde ayarlanır.

Normal kenarlık ve gölge oluşturma yolu, corner-shape değerleri için iyi sonuç veriyordu. Bu değerler yuvarlak veya daha dışbükeydi (ör. squircle). Ayrıca, scoop değerinden daha içbükey şekiller için 90 derece döndürülebiliyordu. Ancak bu varsayılan değer, -1 ile 1 arasındaki corner-shape değerleri için çalışmıyor. Bunun nedeni, kenarlığın veya gölgenin kenara paralel olarak kaydırılmasının, genişliği eşit olmayan bir köşe oluşturmasıdır.

Örneğin, bevel köşesini alıp kenarlığı her iki tarafa doğru birkaç piksel kaydırmak, köşenin ortasının kenarlardan daha geniş göründüğü bir "göbek" efekti oluşturur.

Bunu hesaba katmak için, kontur gibi çalışan bir efekt oluşturulması hedeflenir. Başlangıçtaki köşe eğrisinin normalini bulun ve bunu border veya shadow-spread genişliği kadar uzun yapın.

Neyse ki bu yalnızca alt elipsler (bevel ile yuvarlak arasında) için gereklidir. squircle gibi hiper elipsler beklendiği gibi çalışır.

Bir alt elips eğrisinin normalini bulmak için, alt elipsler ve bunların kuadratik eğri eşdeğerleri birbirine yakın olduğundan kuadratik eğri eşdeğerinin normalini bulmak yeterlidir.

Daha önce hesaplanan aynı yarı köşe kullanılarak aynı orta noktaya sahip bir ikinci dereceden eğri bulunabilir, ikinci dereceden kontrol noktası türetilebilir ve buradan normali hesaplamak kolaydır.

Normal, border-width veya shadow-spread ile aynı uzunlukta devam eder ve ardından sürekli bir yol oluşturmak için ortaya çıkan eğriyi kenarlarla (kenarlık için iç kenar, gölge için dış kenar) kırpar.

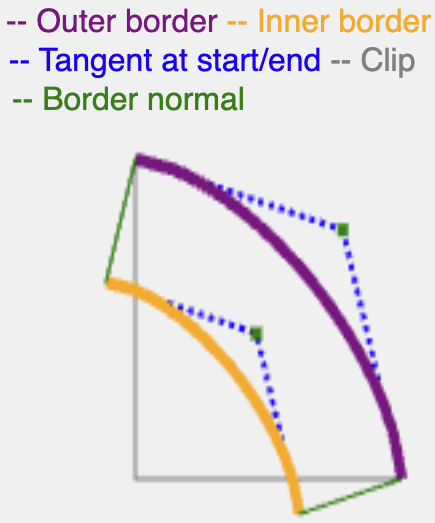
Normalin, sınır şeklini tanımlamak için nasıl genişletildiğini gösteren, sınırlı bir köşenin resmi.
Bu örneği CodePen'de inceleyin.

superellipse için teğet hesaplamanın matematiksel olarak daha doğru yolları olsa da bu yöntem verimlidir ve kenarlıkları ve gölgeleri oluşturmak için yeterli sonuçlar üretir.

Renk birleştirme

Tarayıcılarda gerçekleşen ilginç bir boyama işlemi, CSS'de belirtilmemiştir. Tek tip olmayan renklere veya stillere sahip kenarlıkları oluşturur. Örneğin, öğenizin üst kenarlığı düz yeşil, sağ kenarlığı ise noktalı sarı renkte olabilir. Bu durumlarda gönye, kenarlık kenarının ilgili köşesi ile dolgu kenarının ilgili köşesi arasında uzanan bir kesim çizgisidir. Bitişik kenarlar arasında sınır oluşturur.Belirtilmemiş olsa da oluşturma işlemi tarayıcılar arasında biraz tutarlıdır.

Bu özellik, Blink'te (ve diğer tarayıcılarda) aşağıdaki şekilde uygulanır. Boyanacak kenar, köşede kesişen bir çokgen gibi kabaca kırpılır. Bu işlem, ilgili kenarı içerecek ancak diğer kenarları içermeyecek şekilde hesaplanır. Bu, diğer kenarlardan birinin yanlış stil ve renkle boyanması olan taşmayı önler.

Bu çokgenin hesaplanması şimdiye kadar nispeten basitti. Çünkü düzenli yuvarlatılmış köşelerde köşe alanları asla çakışamaz. Ancak bu durum, hipo-elipslerde ve özellikle içbükey süper elipslerde (negatif superellipse değerleri) değişir. Bu durum, basit kesişim poligonlarının çakışmaya ve "taşmaya" çok yatkın olmasına neden olan oldukça ilginç şekiller oluşturabilir.

Aşağıdaki CSS'yi inceleyin:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}
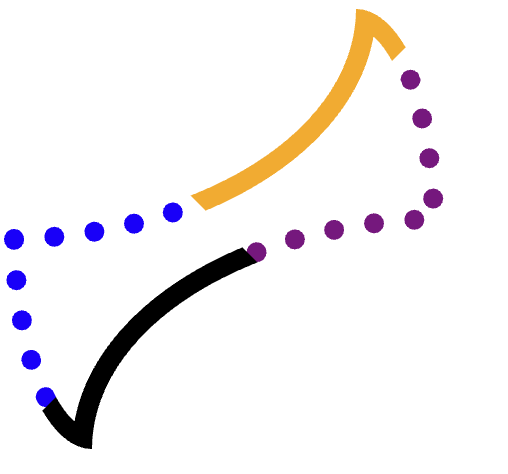
CSS öğesinin, turuncu, mor noktalı, siyah ve mavi noktalı kenarları gösteren, tek tip olmayan kenarlara sahip örneği.

Her kenarı (turuncu, mor noktalı, siyah, mavi noktalı) ayrı ayrı kırpıp ardından yolu çizmek istiyoruz.

Bunu diğer üç köşeyi çakıştırmadan yapmak için dikkatli bir kırpma işlemi gerekir.

Örneğin, turuncu (üst) kenarı ele alalım.

Bu kenarın tamamını içeren ve mor, sarı, hatta siyah kenarlara taşmayan tam bir poligon bulmak zordur. Diğer bazı şekiller daha zordur.

Bu işlem üç klip içerir.

İlk klip, tüm köşeyi (gönye olmadan) içeren kenarın tamamını kapsar. Örneğin:

İki köşeyi (biri kepçe, biri yuvarlak) temsil eden, köşesi kesilmiş bir şekil.

Bu, uçları birleştirilmiş, aralarında minimum kenar bulunan iki köşeden (biri scoop, biri yuvarlak) oluşur.

Bu şekilden başlandığında karşı kenarla çakışmalar ortadan kalkar ve artık yalnızca iki gönye sorun teşkil eder.

Bu, kenar-kenar ve dolgu-kenar köşeleri arasında geçen ve kenarla kesişmek üzereyken duran bir poligonun bu köşeden kırpılmasıyla elde edilir:

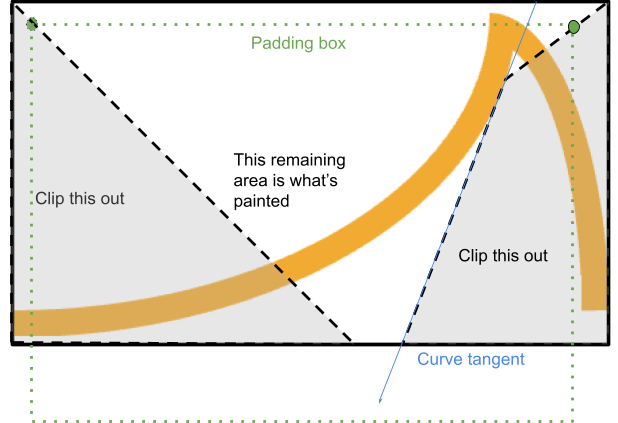
Kırpılacak alanların gösterimi.

Sistem, kenar sınırından dolgu kenarına giden bir çizginin, eğrinin ilgili başlangıç noktasından gelen teğetiyle kesiştiği noktayı bulur (eğri içbükeyse).

Bu nokta oluşturulan alanın içindeyse işlem burada durur ve dörtgeni tamamlayarak kenarlık kutusuyla tekrar buluşana kadar bu teğet boyunca devam eder.

Aksi takdirde, basit bir üçgen kırpılabilir.

Özet

Web platformu, web tasarımcılarına ve geliştiricilere önemli bir ifade gücü sağlar. Bazen tek bir sayısal değer alan bir CSS özelliği, doğru ve tutarlı şekilde oluşturulması için önemli bir karmaşıklığı gizler.

corner-shape özelliği şaşırtıcı derecede karmaşıktı. Bu doküman, Blink'te, diğer tarayıcılarda veya spesifikasyonda bu özellik üzerinde çalışacak gelecekteki geliştiricilere yardımcı olmayı amaçlamaktadır.