Publicado em: 19 de fevereiro de 2026
Um dos recursos de CSS lançados pelo Chrome em 2025 foi o
corner-shape.
Isso permite definir o formato de um canto que tem um border-radius usando
palavras-chave como bevel e scoop. Também é possível usar uma função superellipse que recebe um valor entre -Infinity e Infinity.
Leia o artigo extenso de Amit Sheen no Frontend Masters para ter uma ótima visão geral do recurso e de como ele funciona.
Ao implementar esse recurso no início de 2025, encontrei alguns desafios interessantes de complexidade variada. Aprendi muito sobre superelipses, pintura de bordas no Blink e como usar matemática vetorial para gráficos 2D.
Este documento compartilha algumas das coisas que aprendi, que também podem ser interessantes para outras pessoas.
Simetria de formas convexas e côncavas
Embora os valores de superellipse (k) tradicionalmente variem entre 0 e Infinity, em que os valores entre 0 e 1 são côncavos e o restante é convexo (1 sendo bevel), os valores de superellipse na especificação CSS variam entre -Infinity e Infinity e representam 2k. Isso cria uma simetria, já que qualquer valor positivo parece a imagem espelhada da contraparte negativa.
No entanto, por padrão, a fórmula superellipse não funciona assim.
A fórmula de superellipse é: xk + yk = 1. A fórmula inversa, x1/k + y1/k = 1, não produz uma curva visualmente simétrica.
Por exemplo, com um k de 2:
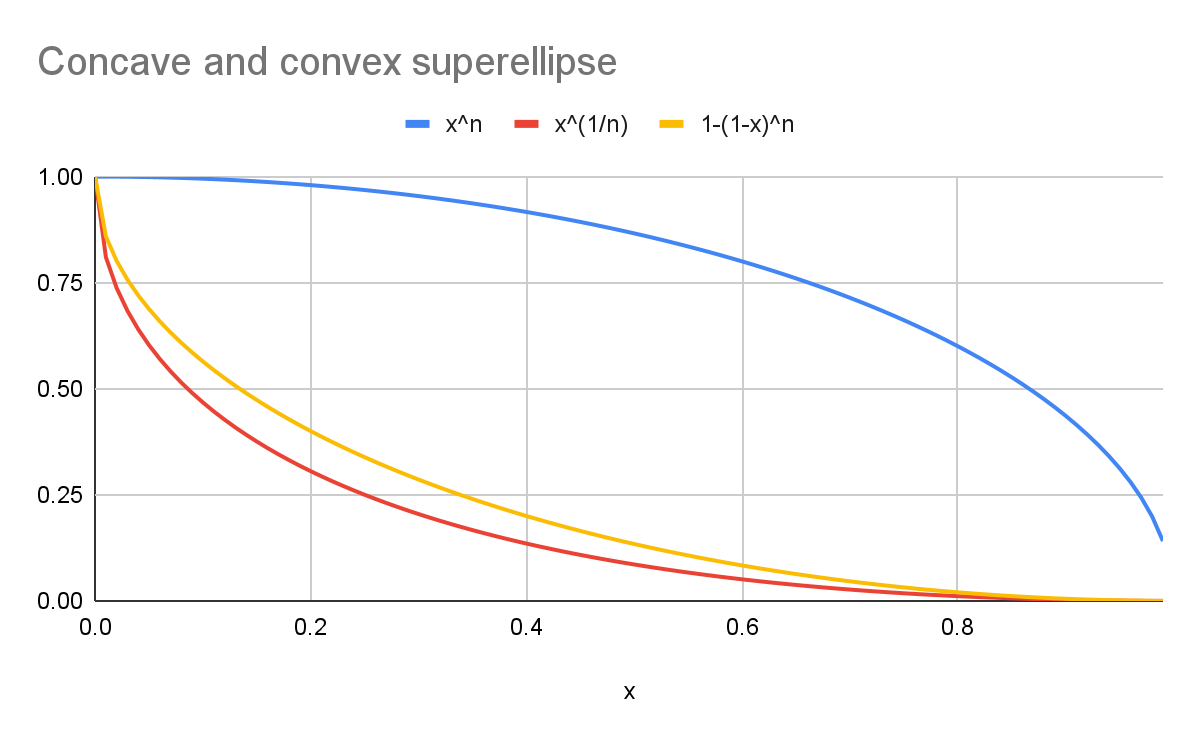
- A curva azul representa um arredondamento
superellipse(y=xn). - A curva vermelha representa uma
scoopsuperellipsecom a fórmula canônica (y=x1/n). - A curva amarela representa uma curva visualmente simétrica à azul (
y=1-(1-x)n).
Como o gráfico mostra, as formas não são iguais.
Não vou me aprofundar na matemática, mas isso tem a ver com normas duais e como percebemos a curvatura.
Em termos de especificação e implementação, estamos representando algo visual aqui. Por isso, usamos os equivalentes simétricos ao calcular formas côncavas. O restante do cálculo é feito em formas convexas (k>=1 ou valores positivos de superelipse).
Fórmula de forma fechada
O próximo desafio é representar a curva, ou o perímetro do
superellipse, na forma fechada, uma fórmula feita de operações aritméticas simples.
Isso é essencial para a performance, permitindo que o sistema transfira a renderização superellipse para o mecanismo gráfico.
Os mecanismos gráficos, como o Skia, conhecem as curvas de Bézier. Portanto, representar um superellipse com um pequeno número de curvas de Bézier que se aproximam do perímetro torna a renderização de uma curva superellipse mais eficiente.
Felizmente, usando a regressão simbólica, podemos encontrar uma fórmula que representa metade de um canto convexo como uma única curva de Bézier cúbica.
Uma curva de Bézier cúbica tem quatro pontos:
- O primeiro ponto é (
0, 1). - O último ponto é o canto da superelipse:
0.51/k,0.51/k. - O primeiro ponto de controle se estende no mesmo nível do ponto inicial: (
a, 1). - O segundo ponto de controle é diagonal ao meio do canto:
(0.51/k - b,0.51/k + b).
O valor de meio canto usado aqui é uma coordenada muito importante que vamos usar para outros cálculos mais adiante.
Em que a e b são calculados com base em k usando regressão simbólica.
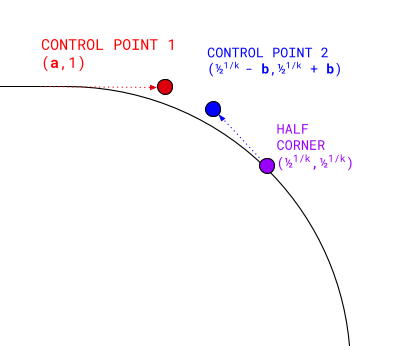
Calcular esses quatro pontos e renderizar uma curva de Bézier cúbica entre eles fornece uma meia esquina convexa de forma fechada com um determinado k. Em seguida, podemos girar os resultados para preencher o restante do canto, aplicar a outros cantos e inverter para renderizar os equivalentes côncavos.
Sem entrar em detalhes matemáticos, a fórmula para calcular a e b é esta:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Bordas e sombras
Além de calcular o caminho do perímetro do canto, o sistema também calcula como ele aparece quando é deslocado para dentro (uma borda ou um box-shadow embutido) ou para fora (um outline ou um box-shadow normal). Em bibliotecas gráficas convencionais, isso é feito por traços.
No entanto, bordas e sombras em CSS têm características de renderização diferentes de traços:
- As bordas não são uniformes.
- Por exemplo, a borda superior pode ter 10 pixels e a direita, 5 pixels, com o canto interpolando entre elas.
- Além disso, eles se movem para dentro, e não para os dois lados.
- Sombras e contornos não são renderizados exatamente como um traço.
- Em vez disso, eles se ajustam para que os cantos apareçam nítidos.
Embora o caminho de renderização de borda e sombra usual funcione bem para valores corner-shape arredondados ou mais convexos do que isso (por exemplo, squircle), e possa ser girado em 90 graus para formas mais côncavas do que um scoop, esse padrão não funciona para valores corner-shape entre -1 e 1, já que o deslocamento da borda ou da sombra paralela à borda produz um canto que parece ter largura desigual.
Por exemplo, pegar um canto bevel e compensar a borda em alguns pixels para os dois lados cria um efeito de "barriga", em que o meio do canto parece mais largo do que as laterais.
Para isso, o objetivo é criar um efeito que funcione como um traço: encontre a normal da curva do canto no início e faça com que ela tenha o mesmo comprimento da largura do border ou shadow-spread.
Felizmente, isso só é necessário para subelipses (entre bevel e redondo), já que hiperelipses como squircle funcionam como esperado.
Para encontrar a normal de uma curva de subelipse, basta encontrar a normal da curva quadrática correspondente, já que as subelipses e seus equivalentes de curva quadrática são próximos entre si.
Usando o mesmo meio canto calculado antes, é possível encontrar uma curva quadrática com o mesmo ponto médio, derivar o ponto de controle quadrático e, a partir daí, calcular a normal é simples.
A normal continua com o mesmo comprimento de border-width ou shadow-spread e corta a curva resultante com as bordas (interna para borda, externa para sombra) para criar um caminho contínuo.
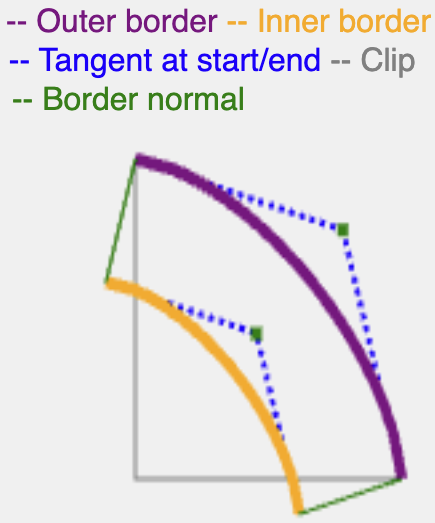
Existem maneiras mais precisas de calcular uma tangente para um superellipse, mas esse método é eficiente e produz resultados adequados para renderizar bordas e sombras.
Junções de cores
Uma parte interessante da renderização que acontece nos navegadores não é especificada em CSS. Ele renderiza bordas com cores ou estilos não uniformes. Por exemplo, quando o elemento tem uma borda superior verde sólida e uma borda direita amarela pontilhada. Nesses casos, o esquadro é uma linha de incisão que vai entre o canto relevante da borda e o canto relevante da margem interna. Ela cria o limite entre as bordas adjacentes.Embora não seja especificado, a renderização é um pouco consistente entre os navegadores.
A maneira como isso é implementado no Blink (e em outros navegadores) é a seguinte. A borda que está prestes a ser pintada é cortada de forma grosseira como um polígono que cruza na esquadria, calculado de forma a incluir a borda relevante, mas não nenhuma das outras bordas. Isso evita o sangramento, pintando uma das outras bordas com o estilo e a cor incorretos.
Até agora, esse polígono era relativamente simples de calcular, porque com cantos arredondados regulares, as áreas dos cantos nunca se sobrepõem. No entanto, isso muda com hipoelipses e, especificamente, com superelipses côncavas (valores negativos de superellipse). Isso pode criar formas bastante interessantes que tornam os polígonos de interseção simples muito propensos a sobreposições e "sangramentos".
Considere o seguinte CSS:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
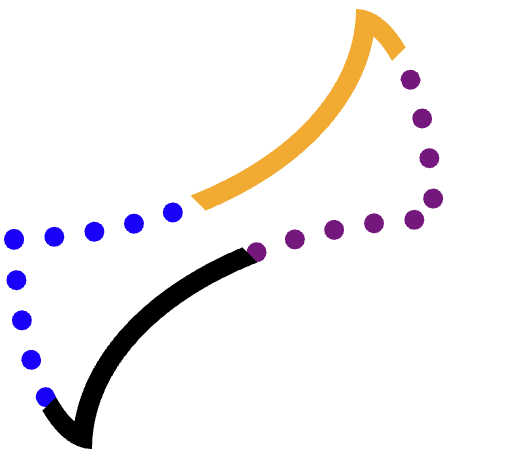
Queremos cortar cada borda (laranja, roxa pontilhada, preta, azul pontilhada) separadamente e depois desenhar o caminho.
Para fazer isso sem sobrepor nenhum dos outros três cantos, é necessário um corte cuidadoso.
Por exemplo, considere a borda laranja (superior).
É difícil encontrar um polígono exato que inclua toda essa borda e não se estenda para as bordas roxas, amarelas ou até pretas. Outras formas são mais desafiadoras.
Esse processo envolve três clipes.
O primeiro clipe inclui toda a borda, com o canto completo (sem um corte em ângulo). Exemplo:

Ele consiste em dois cantos (um scoop e um arredondado), com uma borda mínima entre eles, conectados nas extremidades.
Começar com essa forma elimina as sobreposições com a borda oposta, e agora apenas os dois esquadros continuam sendo uma preocupação.
Isso é feito cortando desse canto um polígono que passa entre os cantos da borda e do padding e para no momento em que está prestes a se cruzar com a borda:
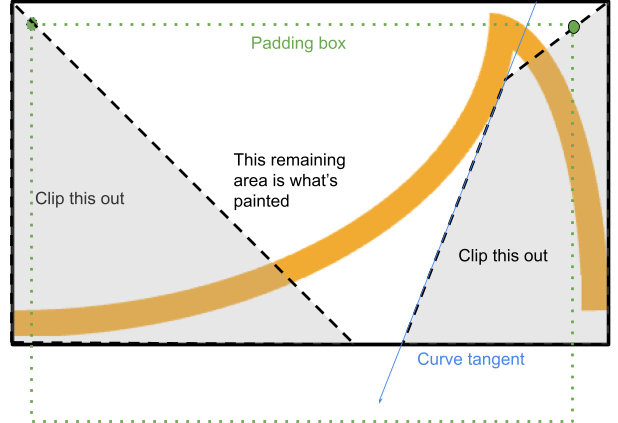
O sistema encontra o ponto em que uma linha da borda até o padding se cruza com a tangente da curva do ponto de partida relevante (se a curva for côncava).
Se esse ponto estiver dentro da área renderizada, o processo será interrompido e continuará ao longo dessa tangente até encontrar a caixa de borda novamente, concluindo um quadrilátero.
Caso contrário, um triângulo simples pode ser cortado.
Resumo
A plataforma da Web oferece aos web designers e desenvolvedores um poder expressivo significativo. Às vezes, uma propriedade CSS que usa um único valor numérico oculta uma complexidade significativa para renderizar com precisão e consistência.
O recurso corner-shape tinha uma complexidade surpreendente. Esta documentação tem como objetivo ajudar futuros desenvolvedores que trabalham nesse recurso no Blink, em outros navegadores ou na especificação.

