Gepubliceerd: 19 februari 2026
Een van de CSS-functies die Chrome in 2025 introduceerde, was corner-shape . Hiermee kun je de vorm van een hoek met een ` border-radius definiëren met behulp van trefwoorden zoals bevel en scoop . Je kunt ook een superellipse functie gebruiken die een waarde tussen -Infinity en Infinity accepteert.
Lees het uitgebreide artikel van Amit Sheen op Frontend Masters voor een uitstekend overzicht van de functie en hoe deze werkt.
Tijdens de implementatie van deze functie begin 2025 stuitte ik op een aantal interessante uitdagingen van verschillende complexiteit. Ik heb veel geleerd over superellipsen, randtekening in Blink en het gebruik van vectormath voor 2D-graphics.
Dit document bevat een aantal dingen die ik heb geleerd en die wellicht ook interessant kunnen zijn voor anderen.
Symmetrie van bolle en holle vormen
Hoewel superellipse ( k ) traditioneel tussen 0 en Infinity liggen, waarbij waarden tussen 0 en 1 concaaf zijn en de rest convex (1 staat voor bevel ), liggen superellipse in de CSS-specificatie tussen -Infinity en Infinity en vertegenwoordigen ze k . Dit creëert een symmetrie, aangezien elke positieve waarde eruitziet als het spiegelbeeld van zijn negatieve tegenhanger.
Standaard werkt de superellipse echter niet op die manier.
De formule superellipse is: x k + y k = 1 De inverse formule, x 1/k + y 1/k = 1 , levert geen visueel symmetrische curve op.
Bijvoorbeeld met een k van 2 :
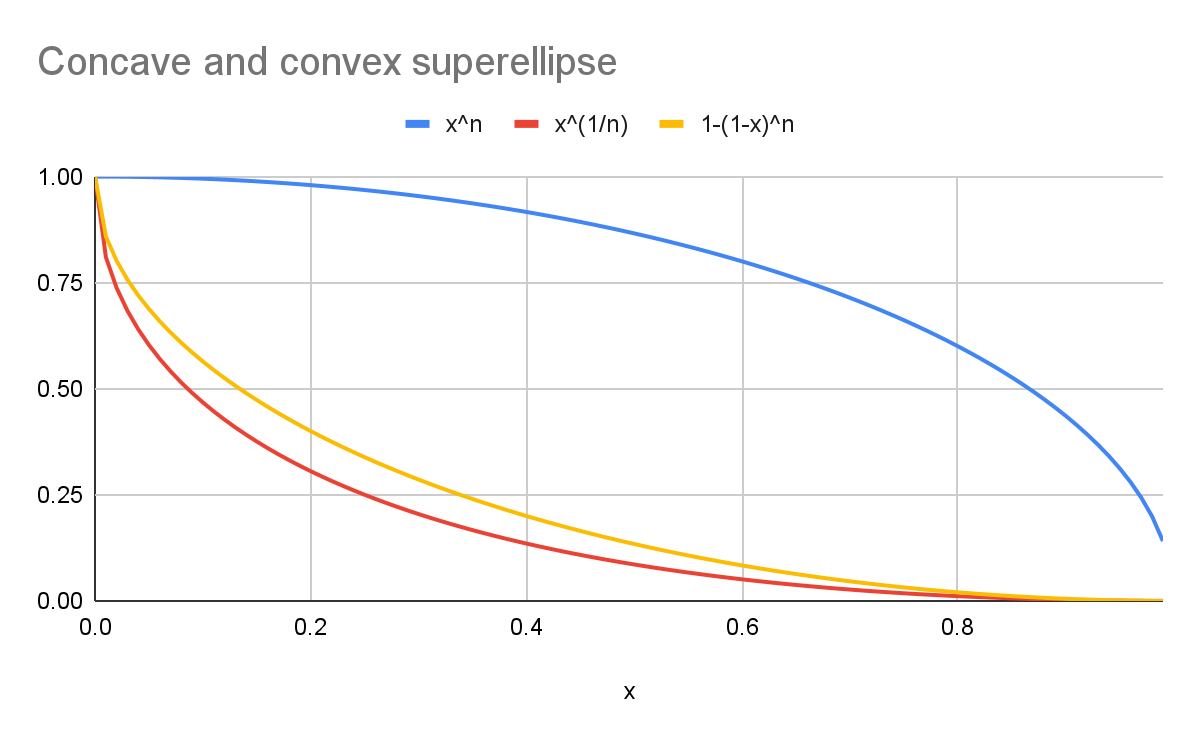
- De blauwe curve stelt een ronde
superellipsevoor (y=x n). - De rode curve stelt een
scoopsuperellipsevoor met de canonische formule (y=x 1/n). - De gele curve vertegenwoordigt een curve die visueel symmetrisch is aan de blauwe curve (
y=1-(1-x) n).
Zoals de grafiek laat zien, zijn de vormen niet hetzelfde!
Ik ga niet dieper in op de wiskunde erachter, maar het heeft te maken met duale normen en hoe we kromming waarnemen.
Wat de specificatie en implementatie betreft, representeren we hier iets visueels, dus gebruiken we de symmetrische equivalenten bij het berekenen van concave vormen. De rest van de wiskundige berekeningen worden uitgevoerd op convexe vormen ( k>=1 , oftewel positieve superellipswaarden).
Gesloten formule
De volgende uitdaging is het weergeven van de curve, oftewel de omtrek van de superellipse , in een gesloten vorm , een formule bestaande uit eenvoudige rekenkundige bewerkingen. Dit is essentieel voor de prestaties, waardoor het systeem de rendering van de superellipse kan overlaten aan de grafische engine.
Grafische engines zoals Skia zijn bekend met Bézier-curven, dus het weergeven van een superellipse met een klein aantal Bézier-curven die de omtrek benaderen, maakt het renderen van een superellipse efficiënter.
Gelukkig kunnen we met behulp van symbolische regressie een formule vinden die de helft van een convexe hoek voorstelt als een enkele kubieke Béziercurve.
Een kubieke Béziercurve heeft vier punten:
- Het eerste punt is (
0, 1). - Het laatste punt is de werkelijke halve hoek van de superellips:
0.5 1/k ,0.5 1/k. - Het eerste controlepunt strekt zich uit op hetzelfde niveau als het beginpunt: (
a, 1). - Het tweede controlepunt bevindt zich diagonaal in de halve hoek:
(0.5 1/k - b,0.5 1/k + b).
De hier gebruikte waarde van de halve hoek is toevallig een zeer belangrijke coördinaat die we later voor andere berekeningen zullen gebruiken.
Waarbij a en b worden berekend uit k met behulp van symbolische regressie.
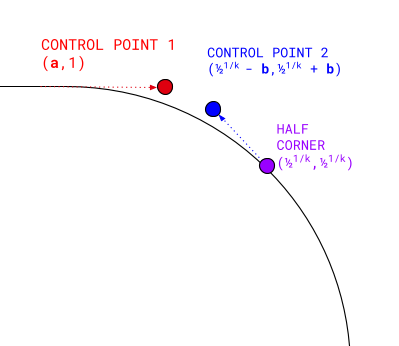
Door deze vier punten te berekenen en een kubieke Béziercurve ertussen te tekenen, verkrijgen we een gesloten, convexe halve hoek met een gegeven k . We kunnen de resultaten vervolgens roteren om de rest van de hoek te vullen, toepassen op andere hoeken en ze spiegelen om de concave equivalenten te tekenen.
Zonder al te diep in de wiskundige details te duiken, is de formule om a en b te berekenen als volgt:
p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086
s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))
a = (logistic - base) / (1 - base)
b = p2 * exp(-p[3] * (s ^ p4))
Grenzen en schaduwen
Naast het berekenen van het pad van de omtrek van de hoek, berekent het systeem ook hoe deze eruitziet wanneer deze naar binnen (een rand of een ingesloten box-shadow ) of naar buiten (een outline of een normale box-shadow ) wordt verschoven. In conventionele grafische bibliotheken wordt dit gedaan door middel van lijntekeningen.
Randen en schaduwen in CSS hebben echter weergavekenmerken die verschillen van lijnen:
- De grenzen zijn niet uniform.
- De bovenrand kan bijvoorbeeld 10 pixels breed zijn en de rechterrand 5 pixels, waarbij de hoek daartussenin wordt geplaatst.
- Bovendien gaan ze naar binnen in plaats van naar beide kanten.
- Schaduwen en contouren worden niet exact hetzelfde weergegeven als een lijn.
- In plaats daarvan passen ze zich aan zodat de hoeken scherp lijken.
Hoewel het gebruikelijke pad voor het renderen van randen en schaduwen goed werkte voor corner-shape die rond of boller zijn (bijvoorbeeld squircle ), en het 90 graden gedraaid kan worden voor vormen die meer concaaf zijn dan een scoop , werkt deze standaardinstelling niet voor corner-shape tussen -1 en 1. Het verschuiven van de rand of schaduw parallel aan de rand resulteert namelijk in een hoek die een ongelijke breedte lijkt te hebben.
Als je bijvoorbeeld een bevel hoek neemt en de rand aan beide kanten een aantal pixels verschuift, ontstaat er een 'buik'-effect, waarbij het midden van de hoek breder lijkt dan de zijkanten.
Om dat te compenseren, is het de bedoeling een effect te creëren dat werkt als een lijn: zoek de normaal van de hoekcurve aan het begin en maak deze even lang als de breedte van de border of shadow-spread .
Gelukkig is dit alleen nodig voor sub-ellipsen (tussen bevel en ronde vormen in), aangezien hyper-ellipsen zoals squircle ) zich gedragen zoals verwacht.
Om de normaal van een subellips te vinden, volstaat het om de normaal van de bijbehorende kwadratische kromme te bepalen, aangezien subellipsen en hun equivalente kwadratische krommen dicht bij elkaar liggen.
Door dezelfde eerder berekende halve hoek te gebruiken, kun je een kwadratische kromme vinden met hetzelfde middelpunt, het bijbehorende kwadratische controlepunt afleiden, en van daaruit is het berekenen van de normaal eenvoudig.
De normaal loopt door met dezelfde lengte als de border-width of shadow-spread , en snijdt vervolgens de resulterende curve af met de randen (binnenrand voor de rand, buitenrand voor de schaduw) om een doorlopend pad te creëren.
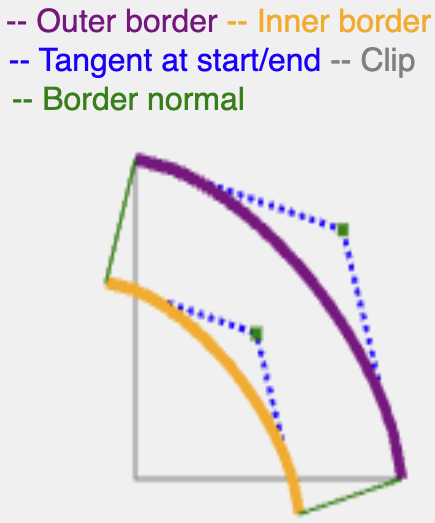
Er bestaan wiskundig nauwkeurigere manieren om de raaklijn aan een superellipse te berekenen, maar deze methode is efficiënt en levert voldoende resultaten op voor het weergeven van randen en schaduwen.
Kleur verbindt
Een interessant detail over het tekenen van randen in browsers is niet gespecificeerd in CSS. Het zorgt ervoor dat randen met niet-uniforme kleuren of stijlen worden weergegeven. Bijvoorbeeld, wanneer een element een groene, effen bovenrand heeft en een gele, gestippelde rechterrand. In deze gevallen is de versteklijn een inkeping die loopt tussen de betreffende hoek van de rand en de betreffende hoek van de opvulling. Deze lijn creëert de grens tussen de aangrenzende randen. Hoewel niet gespecificeerd, is de weergave in verschillende browsers redelijk consistent.
De manier waarop dit in Blink (en in andere browsers) is geïmplementeerd, is als volgt. De rand die op het punt staat te worden getekend, wordt op een grove manier afgesneden, net als een veelhoek die elkaar kruist bij de verstekhoek. Deze afsnijding is zodanig berekend dat de betreffende rand wel wordt meegenomen, maar de andere randen niet. Dit voorkomt dat een van de andere randen met de verkeerde stijl en kleur wordt getekend.
Deze veelhoek was tot nu toe relatief eenvoudig te berekenen, omdat bij regelmatige afgeronde hoeken de hoekvlakken elkaar nooit kunnen overlappen. Dit verandert echter bij hypo-ellipsen en met name bij concave superellipsen (negatieve superellipse ). Deze kunnen behoorlijk interessante vormen creëren, waardoor de eenvoudige intersectie-veelhoeken erg gevoelig worden voor overlappingen en "bloedingen".
Overweeg de volgende CSS:
.weird {
width: 200px;
height: 200px;
corner-shape: scoop round;
border-radius: 80% 20% / 50% 50%;
border-width: 10px;
border-color: orange purple black blue;
border-style: solid dotted;
}
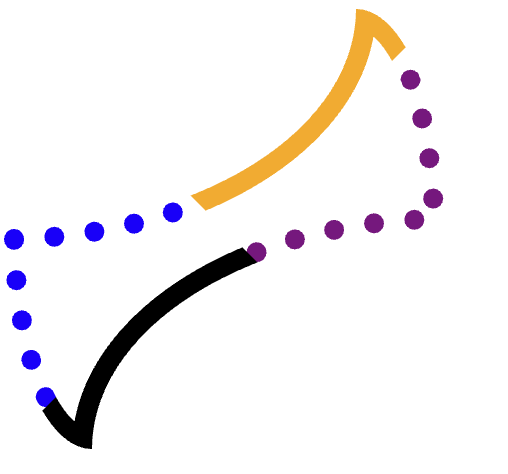
We willen elke rand (oranje, paars gestippeld, zwart, blauw gestippeld) afzonderlijk knippen en vervolgens het pad tekenen.
Om dit te bereiken zonder dat de drie andere hoeken elkaar overlappen, is zorgvuldig knippen noodzakelijk.
Neem bijvoorbeeld de oranje (bovenste) rand.
Het is lastig om een exacte veelhoek te vinden die de hele rand omvat en niet overloopt in de paarse, gele of zelfs zwarte randen. Sommige andere vormen zijn nog lastiger.
Dit proces omvat drie clips.
De eerste clip toont de volledige rand, inclusief de hele hoek (zonder verstek). Bijvoorbeeld:

Dit bestaat uit twee hoeken (een scoop en een ronde), met een minimale rand ertussen, die aan de uiteinden met elkaar verbonden zijn.
Door uit te gaan van deze vorm worden overlappingen met de tegenoverliggende rand geëlimineerd, en blijven alleen de twee verstekken nog een aandachtspunt.
Dit wordt bereikt door vanuit deze hoek een veelhoek uit te knippen die tussen de hoeken van de rand en de opvulrand doorloopt en stopt op het moment dat deze de rand bijna raakt:
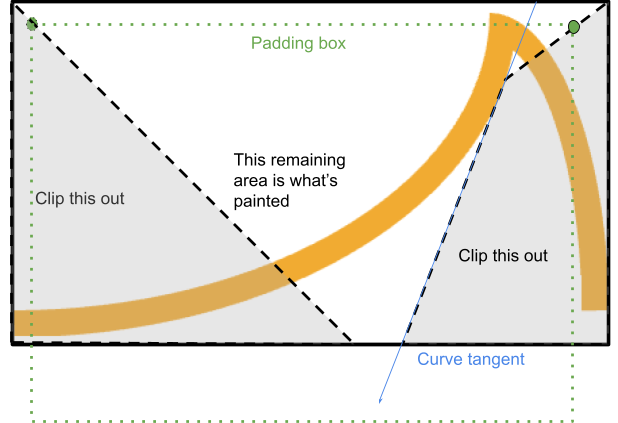
Het systeem vindt het punt waar een lijn van de rand naar de opvulrand de raaklijn van de curve snijdt vanuit het betreffende startpunt (als de curve concaaf is).
Als dat punt zich binnen het weergegeven gebied bevindt, stopt het proces daar en gaat het verder langs die raaklijn totdat het de randbox weer raakt, waarmee een vierhoek wordt voltooid.
Anders kan een eenvoudige driehoek worden bijgesneden.
Samenvatting
Het webplatform biedt webdesigners en -ontwikkelaars aanzienlijke expressieve mogelijkheden. Soms verbergt een CSS-eigenschap die een enkele numerieke waarde accepteert, een aanzienlijke complexiteit achter de schermen om een accurate en consistente weergave te garanderen.
De corner-shape bleek verrassend complex. Deze documentatie is bedoeld om toekomstige ontwikkelaars te helpen die aan deze functionaliteit werken, in Blink, andere browsers of de specificatie.


