ব্লিঙ্কে CSS কর্নার-শেপ বাস্তবায়নের কর্নার কেসগুলি

Noam Rosenthal

প্রকাশিত: ১৯ ফেব্রুয়ারী, ২০২৬

২০২৫ সালে ক্রোম যে CSS ফিচারটি পাঠিয়েছিল তার মধ্যে একটি ছিল corner-shape । এটি আপনাকে bevel এবং scoop এর মতো কীওয়ার্ড ব্যবহার করে border-radius একটি কোণার আকৃতি নির্ধারণ করতে দেয়। আপনি একটি superellipse ফাংশনও ব্যবহার করতে পারেন যা -Infinity এবং Infinity মধ্যে একটি মান গ্রহণ করে।

বৈশিষ্ট্যটি এবং এটি কীভাবে কাজ করে তার একটি দুর্দান্ত ওভারভিউ জানতে ফ্রন্টএন্ড মাস্টার্সে অমিত শিনের বিস্তৃত নিবন্ধটি দেখুন।

২০২৫ সালের গোড়ার দিকে এই বৈশিষ্ট্যটি বাস্তবায়নের সময়, আমি বিভিন্ন জটিলতার কয়েকটি আকর্ষণীয় চ্যালেঞ্জের মুখোমুখি হয়েছিলাম। আমি সুপারএলিপসেস, ব্লিঙ্কে বর্ডার পেইন্টিং এবং 2D গ্রাফিক্সের জন্য ভেক্টর গণিত ব্যবহার সম্পর্কে অনেক কিছু শিখেছি।

এই ডকুমেন্টটি আমার শেখা কিছু জিনিস শেয়ার করে, যা অন্যদের কাছেও আকর্ষণীয় হতে পারে।

উত্তল এবং অবতল আকারের প্রতিসাম্য

যদিও superellipse ( k ) মানগুলি ঐতিহ্যগতভাবে 0 এবং Infinity মধ্যে যায়, যেখানে 0 এবং 1 এর মধ্যে মানগুলি অবতল এবং বাকিগুলি উত্তল (1 হল bevel ), CSS স্পেসিফিকেশনে superellipse মানগুলি -Infinity এবং Infinity এর মধ্যে যায় এবং 2 k প্রতিনিধিত্ব করে। এটি একটি প্রতিসাম্য তৈরি করে কারণ যেকোনো ধনাত্মক মান তার নেতিবাচক প্রতিরূপের আয়না চিত্রের মতো দেখায়।

তবে, ডিফল্টরূপে, superellipse সূত্রটি সেভাবে কাজ করে না।

superellipse সূত্রটি হল: x k + y k = 1 বিপরীত সূত্র, x 1/k + y 1/k = 1 , দৃশ্যত প্রতিসম বক্ররেখা তৈরি করে না।

উদাহরণস্বরূপ, 2 এর k দিয়ে:

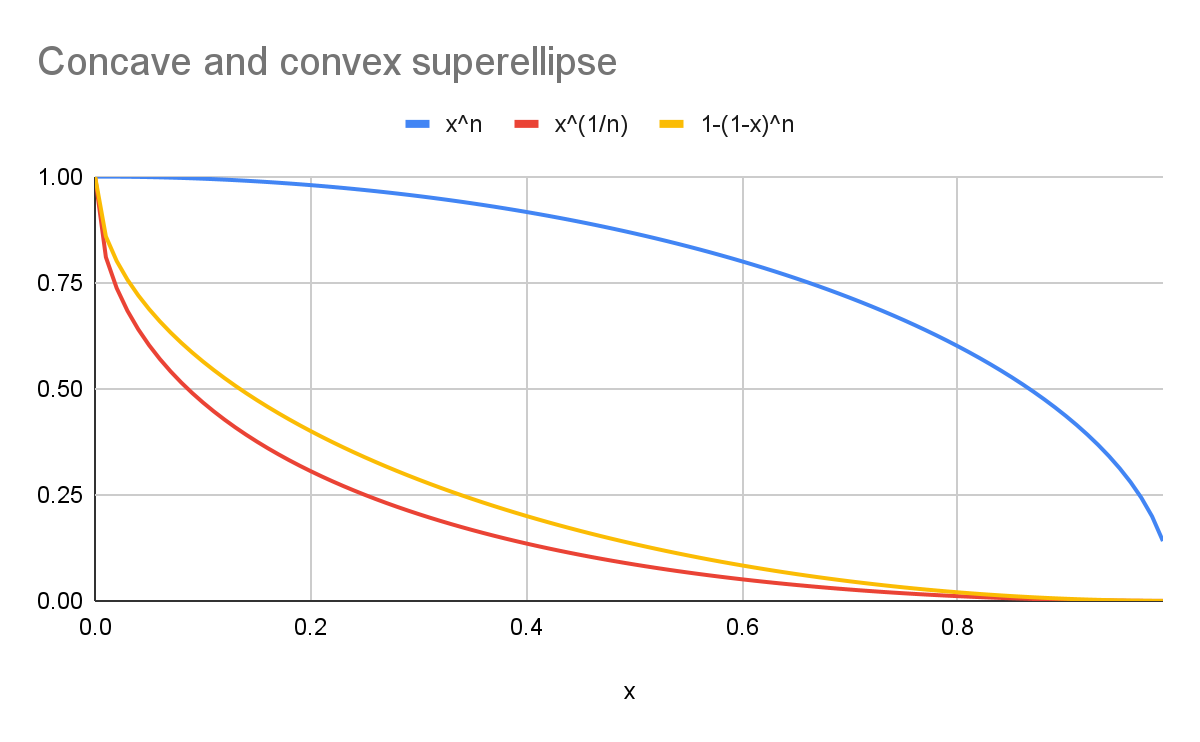
• নীল বক্ররেখাটি একটি বৃত্তাকার superellipse ( y=x n ) প্রতিনিধিত্ব করে।
• লাল বক্ররেখাটি ক্যানোনিকাল সূত্র ( y=x 1/n ) সহ একটি scoop superellipse প্রতিনিধিত্ব করে।
• হলুদ বক্ররেখা এমন একটি বক্ররেখাকে প্রতিনিধিত্ব করে যা নীল বক্ররেখার ( y=1-(1-x) n ) দৃশ্যত প্রতিসম।

চার্টে যেমন দেখা যাচ্ছে, আকৃতিগুলো এক নয়!

আমি এর গণিতে আরও গভীরে যাব না, তবে এটি দ্বৈত মান এবং আমরা কীভাবে বক্রতা উপলব্ধি করি তার সাথে সম্পর্কিত।

স্পেসিফিকেশন এবং বাস্তবায়নের ক্ষেত্রে, আমরা এখানে দৃশ্যমান কিছু উপস্থাপন করছি, তাই অবতল আকার গণনা করার সময় আমরা প্রতিসম সমতুল্য ব্যবহার করি। বাকি গণিত উত্তল আকার ( k>=1 , অথবা ধনাত্মক অতিউপবৃত্তাকার মান) এর উপর করা হয়।

বন্ধ ফর্ম সূত্র

পরবর্তী চ্যালেঞ্জ হল বক্ররেখা, অথবা superellipse পরিধি, বদ্ধ আকারে উপস্থাপন করা, যা সহজ গাণিতিক ক্রিয়াকলাপের মাধ্যমে তৈরি একটি সূত্র। এটি কর্মক্ষমতার জন্য অপরিহার্য, যা সিস্টেমকে গ্রাফিক্স ইঞ্জিনের কাছে superellipse রেন্ডারিং হস্তান্তর করতে দেয়।

স্কিয়ার মতো গ্রাফিক্স ইঞ্জিনগুলি বেজিয়ার কার্ভের সাথে পরিচিত, তাই একটি superellipse তার পরিধির কাছাকাছি অল্প সংখ্যক বেজিয়ার কার্ভ দিয়ে উপস্থাপন করলে একটি superellipse কার্ভ রেন্ডারিং আরও কার্যকর হয়।

সৌভাগ্যবশত, প্রতীকী রিগ্রেশন ব্যবহার করে, আমরা এমন একটি সূত্র খুঁজে পেতে পারি যা একটি একক ঘনক বেজিয়ার বক্ররেখা হিসাবে অর্ধেক উত্তল কোণকে প্রতিনিধিত্ব করে।

একটি ঘনক বেজিয়ার বক্ররেখার চারটি বিন্দু থাকে:

• প্রথম বিন্দু হল ( 0, 1 )।
• শেষ বিন্দুটি হল প্রকৃত উপবৃত্তাকার অর্ধ-কোণ: 0.5 1/k ,0.5 1/k ।
• প্রথম নিয়ন্ত্রণ বিন্দুটি শুরু বিন্দুর একই স্তরে প্রসারিত: ( a, 1 )।
• দ্বিতীয় নিয়ন্ত্রণ বিন্দুটি অর্ধ-কোণে তির্যক: (0.5 1/k - b,0.5 1/k + b) ।

এখানে ব্যবহৃত অর্ধ-কোণার মানটি একটি অত্যন্ত গুরুত্বপূর্ণ স্থানাঙ্ক যা আমরা ভবিষ্যতে অন্যান্য গণনার জন্য ব্যবহার করব।

যেখানে a এবং b প্রতীকী রিগ্রেশন ব্যবহার করে k থেকে গণনা করা হয়।

একটি প্রদর্শনের জন্য, এই কোডপেনটি দেখুন।

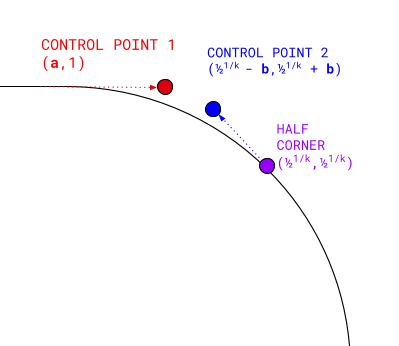
এই চারটি বিন্দু গণনা করে এবং তাদের মধ্যে একটি ঘনক বেজিয়ার বক্ররেখা তৈরি করলে একটি নির্দিষ্ট k সহ একটি বদ্ধ উত্তল অর্ধ কোণ তৈরি হয়। এরপর আমরা ফলাফলগুলি ঘোরাতে পারি যাতে কোণার বাকি অংশটি পূরণ করা যায়, অন্যান্য কোণগুলিতে প্রয়োগ করা যায় এবং অবতল সমতুল্য রেন্ডার করার জন্য সেগুলি উল্টানো যায়।

গাণিতিক জটিলতায় আর না গিয়ে, a এবং b গণনার সূত্রটি হল:

p0 = 1.2430920942724248
p1 = 2.010479023614843
p2 = 0.32922901179443753
p3 = 0.2823023142212073
p4 = 1.3473704261055421
p5 = 2.9149468637949814
p6 = 0.9106507102917086

s = log2(k)
slope = p0 + (p6 - p0) * 0.5 * (1 + tanh(p5 * (s - p1)))
base = 1 / (1 + exp(slope * p1))
logistic = 1 / (1 + exp(slope * (p1 - s)))

a = (logistic - base) / (1 - base)
b =  p2 * exp(-p[3] * (s ^ p4))

সীমানা এবং ছায়া

কোণার পরিধির পথ গণনা করার পাশাপাশি, সিস্টেমটি ভিতরের দিকে (একটি সীমানা বা একটি ইনসেট box-shadow ) অথবা বাইরের দিকে (একটি outline বা একটি সাধারণ box-shadow ) অফসেট করলে এটি কেমন দেখায় তাও গণনা করে। প্রচলিত গ্রাফিক্স লাইব্রেরিতে এটি স্ট্রোক করে করা হয়।

তবে, CSS-এ বর্ডার এবং শ্যাডোর রেন্ডারিং বৈশিষ্ট্য স্ট্রোকিংয়ের থেকে আলাদা:

• সীমানাগুলি অভিন্ন নয়।
• উদাহরণস্বরূপ, উপরের সীমানাটি ১০ পিক্সেল এবং ডান সীমানাটি ৫ পিক্সেল হতে পারে, যার মধ্যে কোণটি ইন্টারপোলেট করে।
• উপরন্তু, তারা উভয় দিকের পরিবর্তে ভিতরের দিকে যায়।
• ছায়া এবং রূপরেখা ঠিক স্ট্রোকের মতো রেন্ডার হয় না।
• পরিবর্তে, তারা এমনভাবে সামঞ্জস্য করে যাতে কোণগুলি তীক্ষ্ণ দেখায়।

যদিও সাধারণ সীমানা এবং ছায়া রেন্ডারিং পাথ corner-shape মানগুলির জন্য ভাল কাজ করে যা গোলাকার বা তার চেয়ে বেশি উত্তল (উদাহরণস্বরূপ, squircle ), এবং এটি একটি scoop এর চেয়ে বেশি অবতল আকৃতির জন্য 90 ডিগ্রি ঘোরানো যেতে পারে, এই ডিফল্টটি -1 এবং 1 এর মধ্যে corner-shape মানগুলির জন্য কাজ করে না, কারণ প্রান্তের সমান্তরাল সীমানা বা ছায়া অফসেট করার ফলে একটি কোণ তৈরি হয় যার প্রস্থ অসম বলে মনে হয়।

উদাহরণস্বরূপ, একটি bevel কর্নার নিয়ে উভয় পাশে কিছু পিক্সেল দিয়ে সীমানা অফসেট করলে একটি "পেট" প্রভাব তৈরি হয়, যেখানে কোণার মাঝখানের অংশটি পাশের চেয়ে প্রশস্ত দেখায়।

এর কারণ হিসেবে, লক্ষ্য হল এমন একটি প্রভাব তৈরি করা যা স্ট্রোকের মতো কাজ করে—শুরুতে কোণার বক্ররেখার স্বাভাবিকতা খুঁজে বের করা এবং এটিকে border বা shadow-spread প্রস্থের সমান লম্বা করা।

সৌভাগ্যবশত, এটি শুধুমাত্র উপ-উপবৃত্তের ( bevel এবং গোলাকার মধ্যে) জন্য প্রয়োজনীয়, কারণ squircle মতো হাইপার-উপবৃত্তগুলি প্রত্যাশা অনুযায়ী কাজ করে।

একটি উপ-উপবৃত্তাকার বক্ররেখার স্বাভাবিক নির্ণয়ের জন্য, এর দ্বিঘাত বক্ররেখার প্রতিরূপের স্বাভাবিক নির্ণয় করা যথেষ্ট, কারণ উপ-উপবৃত্ত এবং তাদের দ্বিঘাত বক্ররেখার সমতুল্য একে অপরের কাছাকাছি।

পূর্বে গণনা করা একই অর্ধ-কোণ ব্যবহার করে, আপনি একটি দ্বিঘাত বক্ররেখা খুঁজে পেতে পারেন যার মধ্যবিন্দু একই, এর দ্বিঘাত নিয়ন্ত্রণ বিন্দু বের করতে পারেন এবং সেখান থেকে স্বাভাবিক গণনা করা সহজ।

normal border-width অথবা shadow-spread এর সমান দৈর্ঘ্য দিয়ে চলতে থাকে, এবং তারপর ফলস্বরূপ বক্ররেখাটিকে প্রান্তের সাথে (অভ্যন্তরীণ প্রান্তকে সীমানার জন্য, বাইরের প্রান্তকে ছায়ার জন্য) ক্লিপ করে একটি অবিচ্ছিন্ন পথ তৈরি করে।

কোডপেনে এই উদাহরণটি দেখুন।

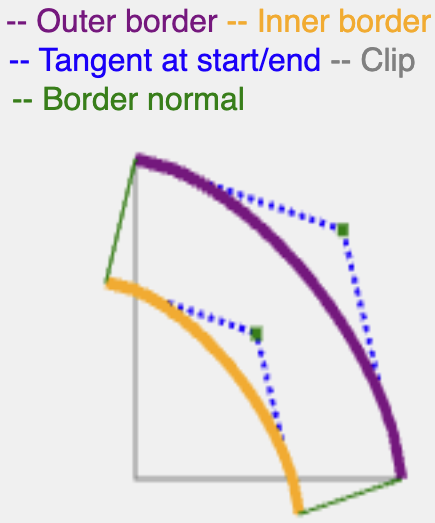
একটি superellipse জন্য একটি ট্যানজেন্ট গণনা করার জন্য আরও গাণিতিকভাবে সঠিক উপায় রয়েছে, তবে এই পদ্ধতিটি দক্ষ এবং সীমানা এবং ছায়া রেন্ডার করার জন্য পর্যাপ্ত ফলাফল দেয়।

রঙের সংযোগ

ব্রাউজারে পেইন্টিংয়ের একটি আকর্ষণীয় অংশ CSS-এ অনির্দিষ্ট থাকে। এটি এমন বর্ডার রেন্ডার করে যার রঙ বা স্টাইল অভিন্ন নয়। উদাহরণস্বরূপ, যেখানে আপনার এলিমেন্টের উপরে সবুজ সলিড বর্ডার এবং ডান দিকে হলুদ ডটেড বর্ডার থাকে। এই ক্ষেত্রে, মিটার হল একটি ইনসিশন লাইন যা বর্ডার এজের প্রাসঙ্গিক কোণ এবং প্যাডিং এজের প্রাসঙ্গিক কোণের মধ্যে যায়। এটি সংলগ্ন প্রান্তগুলির মধ্যে সীমানা তৈরি করে। নির্দিষ্ট না হলেও, রেন্ডারিং ব্রাউজারগুলির মধ্যে কিছুটা সামঞ্জস্যপূর্ণ।

ব্লিঙ্কে (এবং অন্যান্য ব্রাউজারে) এটি যেভাবে বাস্তবায়িত হয় তা নিম্নরূপ। যে প্রান্তটি রঙ করতে চলেছে তা মিটারে ক্রস করা একটি বহুভুজের মতো অশোধিতভাবে ক্লিপ করা হয়েছে, এমনভাবে গণনা করা হয়েছে যাতে এতে প্রাসঙ্গিক প্রান্তটি অন্তর্ভুক্ত থাকে কিন্তু অন্য কোনও প্রান্ত অন্তর্ভুক্ত না হয়। এটি রক্তপাত এড়ায়, অন্য প্রান্তগুলির একটিকে ভুল স্টাইল এবং রঙ দিয়ে রঙ করে।

এই বহুভুজটি গণনা করা এতদিন তুলনামূলকভাবে সহজ ছিল, কারণ নিয়মিত গোলাকার কোণগুলির সাথে কোণার অঞ্চলগুলি কখনই ওভারল্যাপ করতে পারে না। তবে, এটি হাইপো-উপবৃত্তের সাথে এবং বিশেষ করে অবতল সুপৃষ্ঠের (ঋণাত্মক superellipse মান) সাথে পরিবর্তিত হয়। এগুলি বেশ আকর্ষণীয় আকার তৈরি করতে পারে যা সরল ছেদ বহুভুজগুলিকে ওভারল্যাপ এবং "রক্তপাত" হওয়ার ঝুঁকিতে ফেলে।

নিম্নলিখিত CSS বিবেচনা করুন:

.weird {
  width: 200px;
  height: 200px;
  corner-shape: scoop round;
  border-radius: 80% 20% / 50% 50%;
  border-width: 10px;
  border-color: orange purple black blue;
  border-style: solid dotted;
}

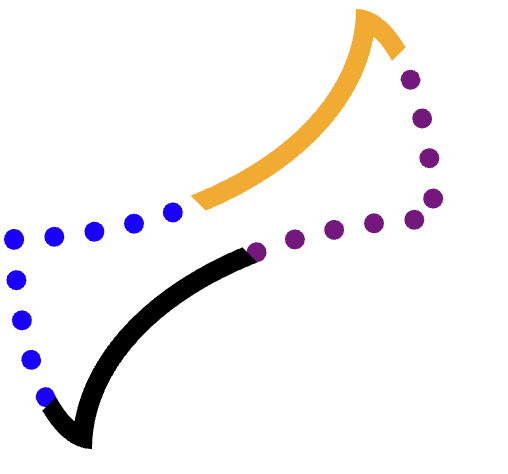
আমরা প্রতিটি প্রান্ত (কমলা, বেগুনি-বিন্দুযুক্ত, কালো, নীল-বিন্দুযুক্ত) আলাদাভাবে ক্লিপ করতে চাই, এবং তারপর পথটি আঁকতে চাই।

অন্য তিনটি কোণকে ওভারল্যাপ না করে এটি অর্জন করার জন্য, সাবধানে ক্লিপিং করা প্রয়োজন।

উদাহরণস্বরূপ, কমলা (উপরের) প্রান্তটি বিবেচনা করুন।

এমন একটি সঠিক বহুভুজ খুঁজে পাওয়া কঠিন যেখানে পুরো প্রান্তটি অন্তর্ভুক্ত থাকে এবং বেগুনি, হলুদ, এমনকি কালো প্রান্তেও প্রবাহিত না হয়। কিছু অন্যান্য আকার আরও চ্যালেঞ্জিং।

এই প্রক্রিয়াটিতে তিনটি ক্লিপ জড়িত।

প্রথম ক্লিপে পুরো প্রান্তটি অন্তর্ভুক্ত রয়েছে, পুরো কোণটি সহ (কোনও মিটার ছাড়াই)। উদাহরণস্বরূপ:

এটি দুটি কোণ (একটি scoop , এক গোলাকার) নিয়ে গঠিত, যার মধ্যে ন্যূনতম প্রান্ত থাকে, প্রান্তে সংযুক্ত থাকে।

এই আকৃতি থেকে শুরু করলে বিপরীত প্রান্তের ওভারল্যাপ দূর হয়, এবং এখন কেবল দুটি মিটারই উদ্বেগের বিষয়।

এই কোণ থেকে ক্লিপিং করে এটি অর্জন করা হয়, একটি বহুভুজ যা বর্ডার-এজ এবং প্যাডিং-এজ কোণগুলির মধ্যে দিয়ে যায় এবং প্রান্তের সাথে ছেদ করার মুহূর্তে থেমে যায়:

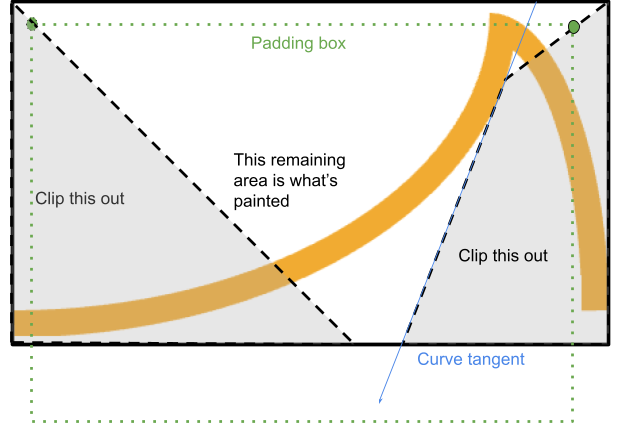
সিস্টেমটি সেই বিন্দুটি খুঁজে বের করে যেখানে সীমানা প্রান্ত থেকে প্যাডিং প্রান্ত পর্যন্ত একটি রেখা প্রাসঙ্গিক শুরু বিন্দু থেকে বক্ররেখার ট্যানজেন্টের সাথে ছেদ করে (যদি বক্ররেখাটি অবতল হয়)।

যদি সেই বিন্দুটি রেন্ডার করা এলাকার ভিতরে থাকে, তাহলে প্রক্রিয়াটি সেখানেই থেমে যায় এবং সেই ট্যানজেন্ট বরাবর চলতে থাকে যতক্ষণ না এটি আবার সীমানা বাক্সের সাথে মিলিত হয়, একটি চতুর্ভুজ সম্পূর্ণ করে।

অন্যথায়, একটি সরল ত্রিভুজ কেটে ফেলা যেতে পারে।

সারাংশ

ওয়েব প্ল্যাটফর্ম ওয়েব ডিজাইনার এবং ডেভেলপারদের উল্লেখযোগ্য প্রকাশ ক্ষমতা প্রদান করে। কখনও কখনও একটি সিএসএস প্রোপার্টি যা একটি একক সংখ্যাসূচক মান নেয় তা হুডের নীচে উল্লেখযোগ্য জটিলতা লুকিয়ে রাখে যাতে এটি সঠিকভাবে এবং ধারাবাহিকভাবে রেন্ডার হয়।

corner-shape বৈশিষ্ট্যটি আশ্চর্যজনক জটিলতা ধারণ করেছিল। এই ডকুমেন্টেশনের লক্ষ্য হল ভবিষ্যতের ডেভেলপারদের সাহায্য করা যারা এই বৈশিষ্ট্যটি নিয়ে কাজ করেন, ব্লিঙ্ক, অন্যান্য ব্রাউজারে, অথবা স্পেসিফিকেশনে।