Este documento es una continuación de WebAssembly y WebGPU para una IA web más rápida, parte 1. Te recomendamos que leas esta publicación o mires la charla en IO 24 antes de continuar.
WebGPU
WebGPU les brinda a las aplicaciones web acceso al hardware de la GPU del cliente para realizar un procesamiento eficiente y altamente paralelo. Desde que lanzamos WebGPU en Chrome, hemos visto demostraciones increíbles de inteligencia artificial (IA) y aprendizaje automático (AA) en la Web.
Por ejemplo, Web Stable Diffusion demostró que era posible usar la IA para generar imágenes a partir de texto, directamente en el navegador. A principios de este año, el equipo de Mediapipe de Google publicó compatibilidad experimental con la inferencia de modelos de lenguaje extenso.
En la siguiente animación, se muestra Gemma, el modelo de lenguaje grande (LLM) de código abierto de Google, que se ejecuta completamente en el dispositivo en Chrome, en tiempo real.
La siguiente demo de Hugging Face del modelo Segment Anything de Meta produce máscaras de objetos de alta calidad por completo en el cliente.
Estos son solo algunos de los increíbles proyectos que muestran el poder de WebGPU para la IA y el AA. WebGPU permite que estos modelos y otros se ejecuten mucho más rápido que en la CPU.
La comparativa de WebGPU para la incorporación de texto de Hugging Face demuestra una gran aceleración en comparación con una implementación de CPU del mismo modelo. En una laptop Apple M1 Max, WebGPU fue más de 30 veces más rápida. Otros informaron que WebGPU acelera la comparativa más de 120 veces.
Mejoras en las funciones de WebGPU para la IA y el AA
WebGPU es excelente para los modelos de IA y AA, que pueden tener miles de millones de parámetros, gracias a la compatibilidad con los shaders de procesamiento. Los sombreadores de cómputo se ejecutan en la GPU y ayudan a ejecutar operaciones de array en paralelo en grandes volúmenes de datos.
Entre las numerosas mejoras que se implementaron en WebGPU durante el último año, seguimos agregando más funciones para mejorar el rendimiento de la IA y el procesamiento de datos en la Web. Recientemente, lanzamos dos funciones nuevas: productos punto de números enteros empaquetados y de punto flotante de 16 bits.
Número de punto flotante de 16 bits
Recuerda que las cargas de trabajo de AA no requieren precisión. shader-f16 es una función que permite usar el tipo f16 en el lenguaje de sombreado de WebGPU. Este tipo de punto flotante ocupa 16 bits, en lugar de los 32 bits habituales. f16 tiene un rango más pequeño y es menos preciso, pero para muchos modelos de IA, esto es suficiente.
Esta función aumenta la eficiencia de las siguientes maneras:
Memoria reducida: Los tensores con elementos f16 ocupan la mitad del espacio, lo que reduce a la mitad el uso de la memoria. Los cálculos de la GPU suelen tener un cuello de botella en el ancho de banda de la memoria, por lo que la mitad de la memoria puede significar que los sombreadores se ejecutan dos veces más rápido. Técnicamente, no necesitas f16 para ahorrar ancho de banda de memoria. Es posible almacenar los datos en un formato de baja precisión y, luego, expandirlos a f32 completo en el sombreador para el procesamiento. Sin embargo, la GPU gasta potencia de procesamiento adicional para empaquetar y desempaquetar los datos.
Reducción de la conversión de datos: f16 usa menos procesamiento minimizando la conversión de datos. Los datos de baja precisión se pueden almacenar y, luego, usar directamente sin conversión.
Mayor paralelismo: Las GPUs modernas pueden ajustar más valores de forma simultánea en las unidades de ejecución de la GPU, lo que le permite realizar una mayor cantidad de cálculos en paralelo. Por ejemplo, una GPU que admite hasta 5 billones de operaciones de punto flotante f32 por segundo podría admitir 10 billones de operaciones de punto flotante f16 por segundo.
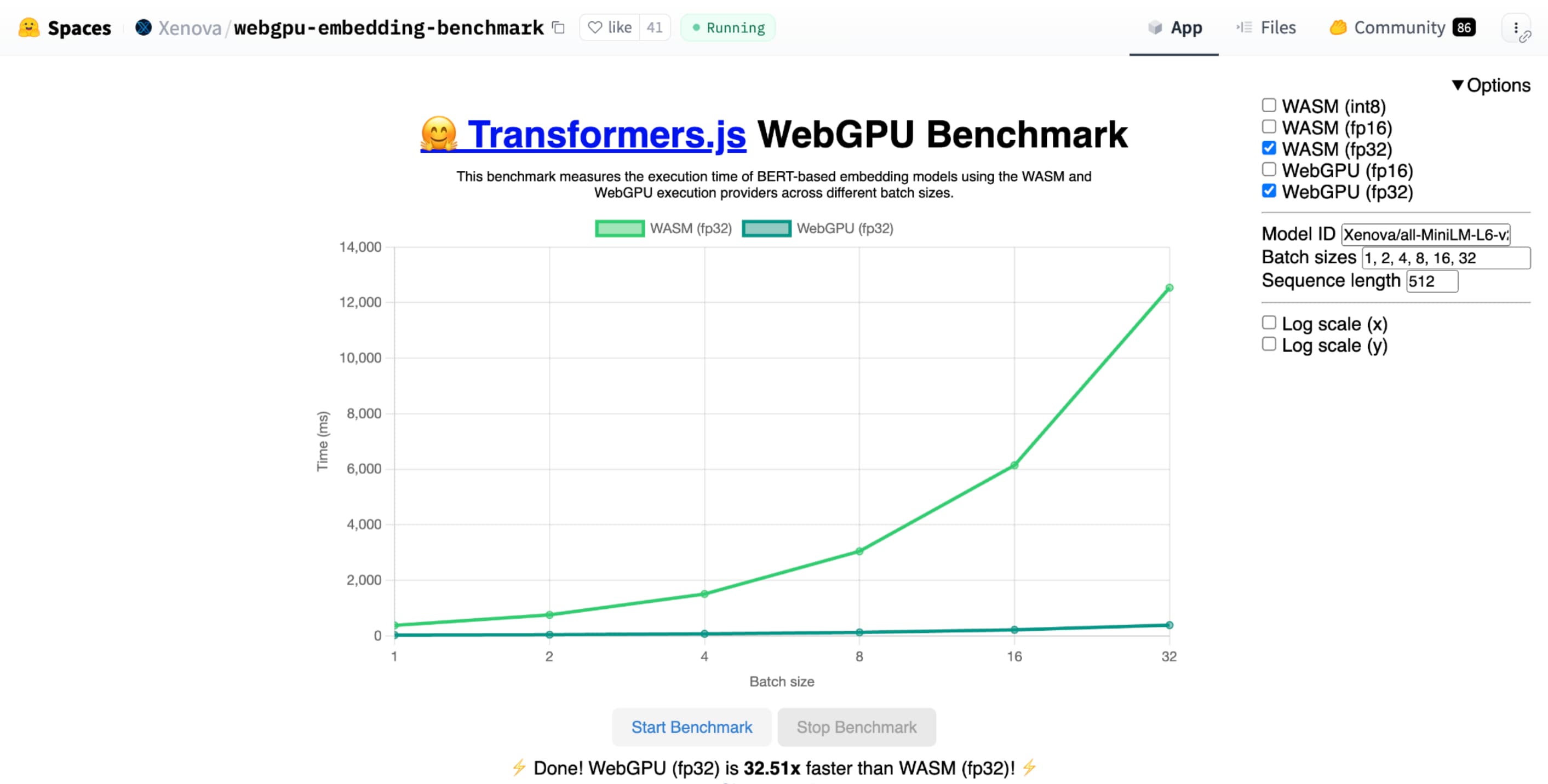
shader-f16, la comparativa de WebGPU para la incorporación de texto de Hugging Face ejecuta la comparativa 3 veces más rápido que f32 en la laptop Apple M1 Max.
WebLLM es un proyecto que puede ejecutar varios modelos grandes de lenguaje. Usa Apache TVM, un framework de compilador de aprendizaje automático de código abierto.
Le pedí al WebLLM que planificara un viaje a París con el modelo de ocho mil millones de parámetros de Llama 3. Los resultados muestran que, durante la fase de precarga del modelo, f16 es 2.1 veces más rápido que f32. Durante la fase de decodificación, es más de 1.3 veces más rápido.
Las aplicaciones primero deben confirmar que el adaptador de GPU admita f16 y, si está disponible, habilitarlo de forma explícita cuando soliciten un dispositivo de GPU. Si no se admite f16, no puedes solicitarlo en el array requiredFeatures.
// main.js
const adapter = await navigator.gpu.requestAdapter();
const supportsF16 = adapter.features.has('shader-f16');
if (supportsF16) {
// Use f16.
const device = await adapter.requestDevice({
requiredFeatures: ['shader-f16'],
});
initApp(device);
}
Luego, en tus sombreadores de WebGPU, debes habilitar f16 de forma explícita en la parte superior. Después de eso, puedes usarlo dentro del sombreador como cualquier otro tipo de datos de número de punto flotante.
// my-shader.wgsl
enable f16;
struct Data {
values : array<vec4<f16>>
}
@group(0) @binding(0) var<storage, read> data : Data;
@compute @workgroup_size(64) fn main(@builtin(global_invocation_id) gid : vec3u) {
let value : vec4<f16> = data.values[gid.x];
...
}
Productos punto de números enteros empaquetados
Muchos modelos aún funcionan bien con solo 8 bits de precisión (la mitad de f16). Esto es popular entre los LLM y los modelos de imágenes para la segmentación y el reconocimiento de objetos. Dicho esto, la calidad de los resultados de los modelos se degrada con menos precisión, por lo que la cuantización de 8 bits no es adecuada para todas las aplicaciones.
Pocas GPUs admiten de forma nativa valores de 8 bits. Aquí es donde entran en juego los productos punto de números enteros empaquetados. Enviamos DP4a en Chrome 123.
Las GPUs modernas tienen instrucciones especiales para tomar dos números enteros de 32 bits, interpretarlos como 4 números enteros de 8 bits empaquetados de forma consecutiva y calcular el producto punto entre sus componentes.
Esto es particularmente útil para la IA y el aprendizaje automático, ya que los kernels de multiplicación de matrices se componen de muchos productos punto.
Por ejemplo, multipliquemos una matriz de 4 × 8 por un vector de 8 × 1. Para calcular esto, se deben tomar 4 productos punto para calcular cada uno de los valores del vector de salida: A, B, C y D.
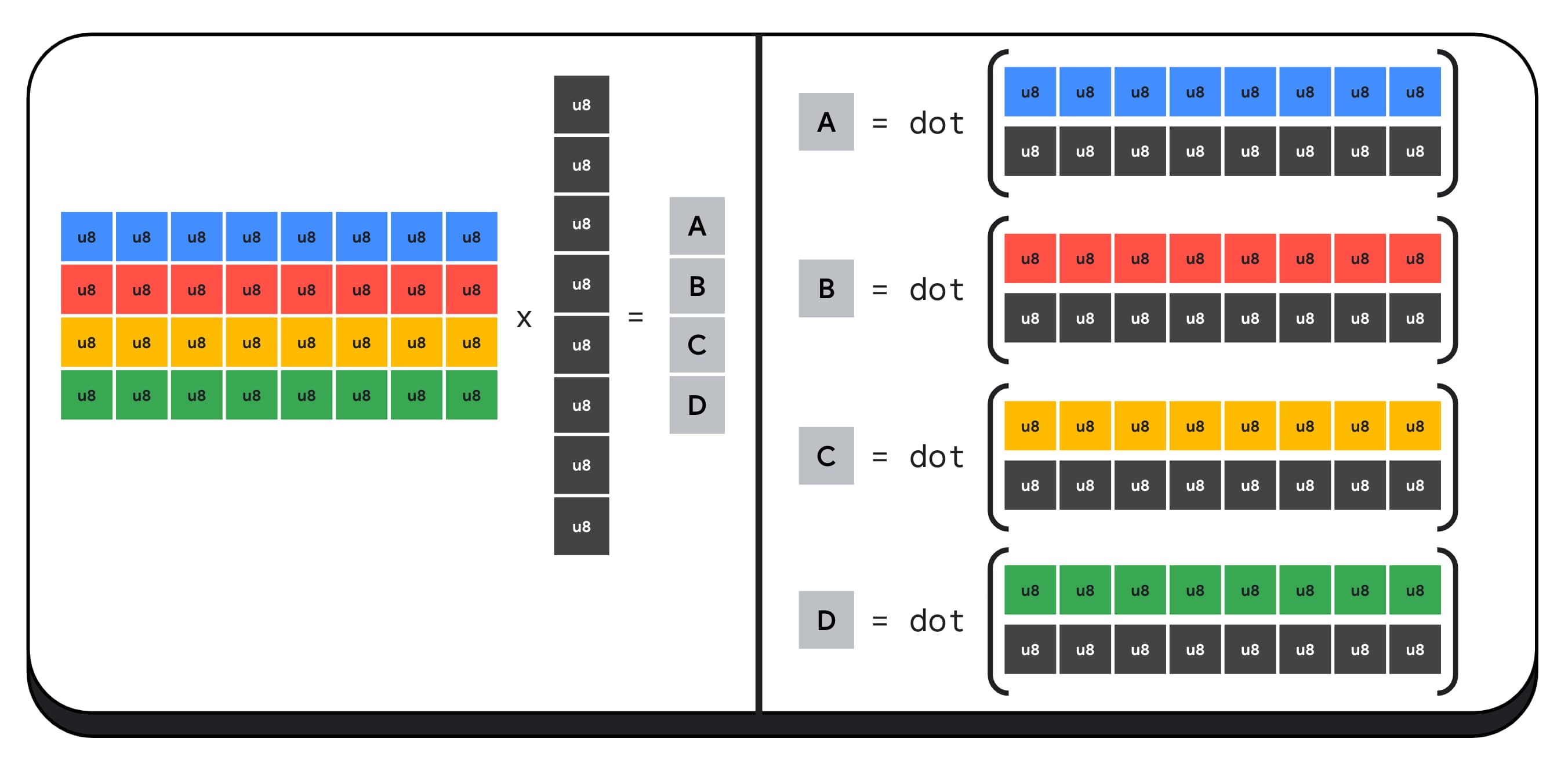
El proceso para calcular cada uno de estos resultados es el mismo. Analizaremos los pasos involucrados en el cálculo de uno de ellos. Antes de realizar cualquier cálculo, primero debemos convertir los datos de número entero de 8 bits a un tipo con el que podamos realizar operaciones aritméticas, como f16. Luego, ejecutamos una multiplicación por elemento y, por último, sumamos todos los productos. En total, para toda la multiplicación de matrices y vectores, realizamos 40 conversiones de números enteros a números de punto flotante para descomprimir los datos, 32 multiplicaciones de números de punto flotante y 28 sumas de números de punto flotante.
En el caso de matrices más grandes con más operaciones, los productos punto de números enteros empaquetados pueden ayudar a reducir la cantidad de trabajo.
Para cada una de las salidas del vector de resultados, realizamos dos operaciones de producto punto empaquetadas con el dot4U8Packed integrado en el lenguaje de sombreado de WebGPU y, luego, sumamos los resultados. En total, para toda la multiplicación de matrices y vectores, no realizamos ninguna conversión de datos. Ejecutamos 8 productos punto empaquetados y 4 sumas de números enteros.

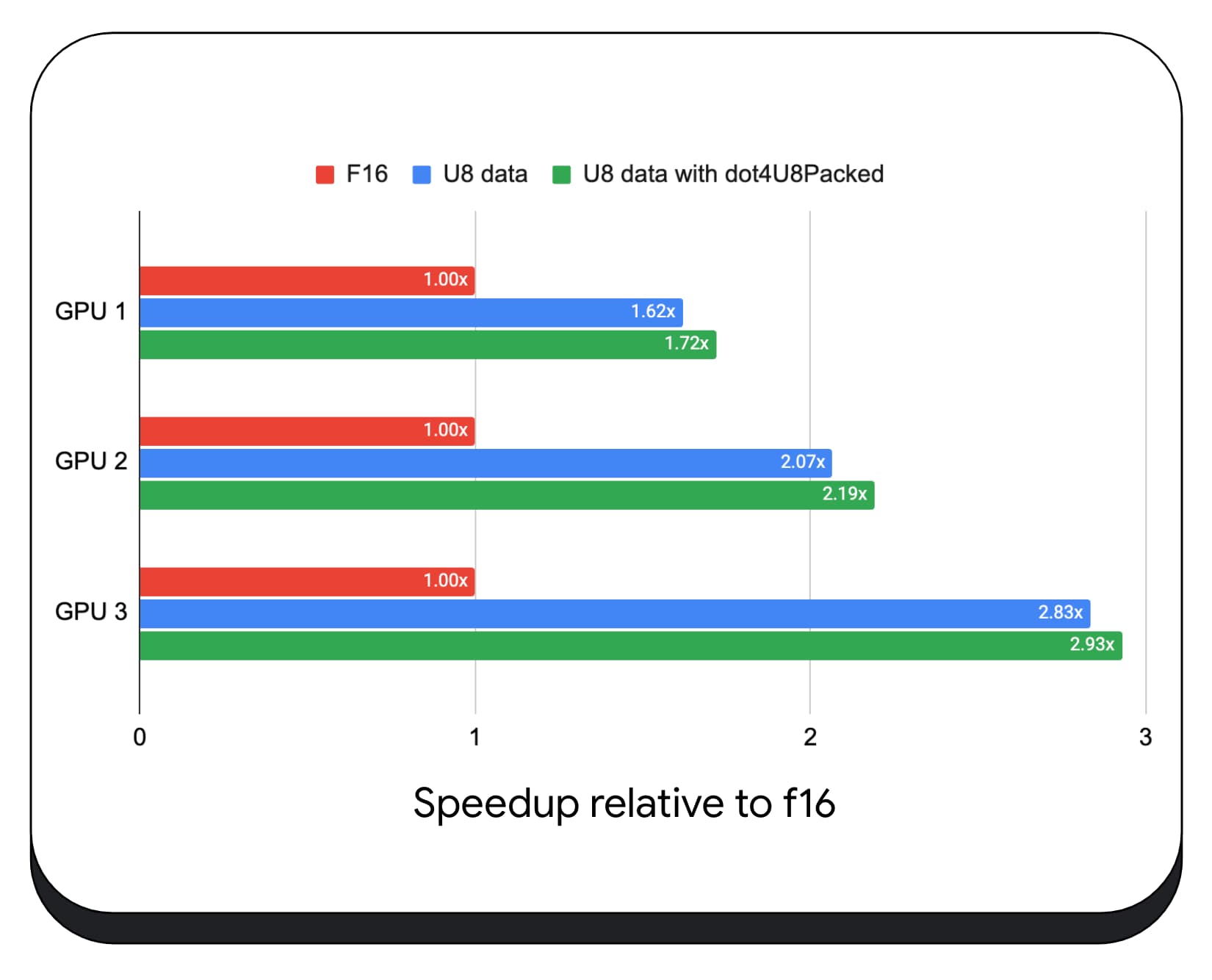
Probamos productos punto enteros empaquetados con datos de 8 bits en una variedad de GPUs para consumidores. En comparación con el punto flotante de 16 bits, podemos ver que el de 8 bits es de 1.6 a 2.8 veces más rápido. Cuando, además, usamos productos punto de números enteros empaquetados, el rendimiento es aún mejor. Es de 1.7 a 2.9 veces más rápido.
Verifica la compatibilidad del navegador con la propiedad wgslLanguageFeatures. Si la GPU no admite productos de punto empaquetados de forma nativa, el navegador polyfilla su propia implementación.
// main.js
if (navigator.gpu.wgslLanguageFeatures.has('packed_4x8_integer_dot_product')) {
// Use dot4U8Packed, dot4I8Packed builtin
// functions in the shaders.
}
La siguiente diferencia de fragmento de código destaca los cambios necesarios para usar productos enteros empaquetados en un sombreador de WebGPU.
Antes: Es un sombreador de WebGPU que acumula productos punto parciales en la variable "sum". Al final del bucle, "sum" contiene el producto punto completo entre un vector y una fila de la matriz de entrada.
// my-dot-product.wgsl @compute @workgroup_size(64) fn main(@builtin(global_invocation_id) gid : vec3u) { var sum : f16; let start = gid.x * uniforms.dim; for (var i = 0u; i < uniforms.dim; i++) { let v1 : vec4<f16> = vector.values[i]; let v2 : vec4<f16> = matrix.values[start + i]; sum += dot(v1, v2); } }
Después: Es un sombreador de WebGPU escrito para usar productos punto enteros empaquetados. La diferencia principal es que, en lugar de cargar 4 valores de punto flotante del vector y la matriz, este sombreador carga un solo número entero de 32 bits. Este número entero de 32 bits contiene los datos de cuatro valores enteros de 8 bits. Luego, llamamos a dot4U8Packed para calcular el producto punto de los dos valores.
// my-dot-product.wgsl
@compute @workgroup_size(64)
fn main(@builtin(global_invocation_id) gid : vec3u) {
var sum : f32;
let start = gid.x * uniforms.dim;
for (var i = 0u; i < uniforms.dim; i++) {
let v1 : u32 = vector.values[i];
let v2 : u32 = matrix.values[start + i];
sum += dot4U8Packed(v1, v2);
}
}
Los productos punto de punto de números enteros empaquetados y de punto flotante de 16 bits son las funciones enviadas en Chrome que aceleran la IA y el AA. El punto flotante de 16 bits está disponible cuando el hardware lo admite, y Chrome implementa productos punto enteros empaquetados en todos los dispositivos.
Puedes usar estas funciones en Chrome estable hoy mismo para obtener un mejor rendimiento.
Funciones propuestas
En el futuro, investigaremos dos funciones más: subgrupos y multiplicación de matrices cooperativas.
La función de subgrupos permite que el paralelismo a nivel de SIMD se comunique o realice operaciones matemáticas colectivas, como una suma de más de 16 números. Esto permite un uso compartido de datos eficiente entre subprocesos. Los subgrupos son compatibles con las APIs de GPUs modernas, con nombres variados y en formas ligeramente diferentes.
Extrajimos el conjunto común en una propuesta que llevamos al grupo de estandarización de WebGPU. Además, creamos prototipos de subgrupos en Chrome con una marca experimental y llevamos nuestros resultados iniciales a la discusión. El problema principal es cómo garantizar un comportamiento portátil.
La multiplicación de matrices cooperativa es una incorporación más reciente a las GPUs. Una multiplicación de matrices grande se puede desglosar en varias multiplicaciones de matrices más pequeñas. La multiplicación de matrices cooperativa realiza multiplicaciones en estos bloques más pequeños de tamaño fijo en un solo paso lógico. Dentro de ese paso, un grupo de subprocesos coopera de manera eficiente para calcular el resultado.
Realizamos una encuesta sobre la compatibilidad en las APIs subyacentes de la GPU y planeamos presentar una propuesta al grupo de estandarización de WebGPU. Al igual que con los subgrupos, esperamos que gran parte del debate se centre en la portabilidad.
Para evaluar el rendimiento de las operaciones de subgrupos, en una aplicación real, integramos la compatibilidad experimental con subgrupos en MediaPipe y la probamos con el prototipo de Chrome para operaciones de subgrupos.
Usamos subgrupos en los kernels de GPU de la fase de precarga del modelo de lenguaje grande, por lo que solo informo la aceleración de la fase de precarga. En una GPU Intel, observamos que los subgrupos tienen un rendimiento dos veces y media más rápido que el modelo de referencia. Sin embargo, estas mejoras no son coherentes entre las diferentes GPUs.
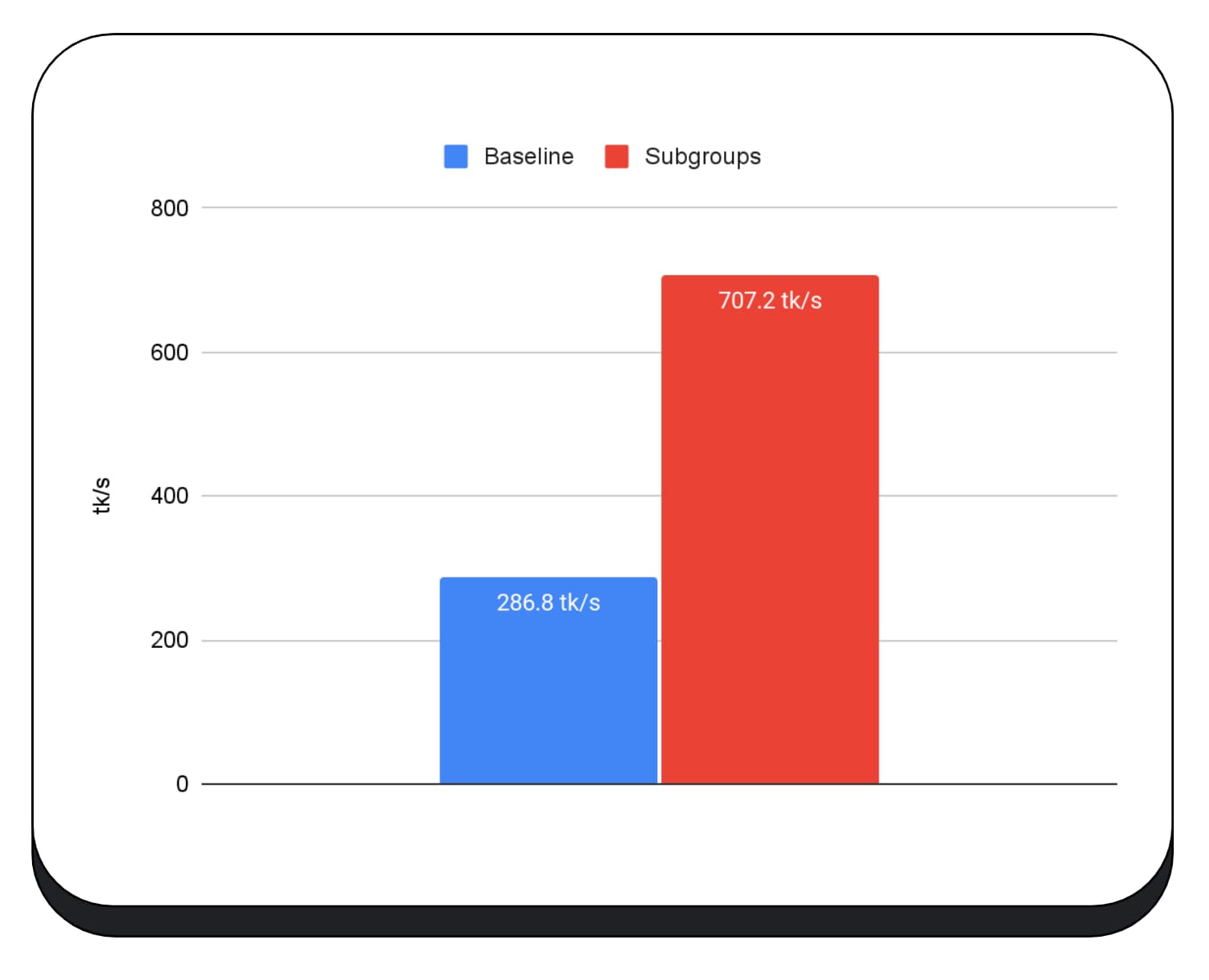
En el siguiente gráfico, se muestran los resultados de aplicar subgrupos para optimizar una microcomparativa de multiplicación de matrices en varias GPUs para consumidores. La multiplicación de matrices es una de las operaciones más pesadas en los modelos de lenguaje grandes. Los datos muestran que, en muchas de las GPUs, los subgrupos aumentan la velocidad dos, cinco y hasta trece veces el modelo de referencia. Sin embargo, observa que, en la primera GPU, los subgrupos no son mucho mejores.
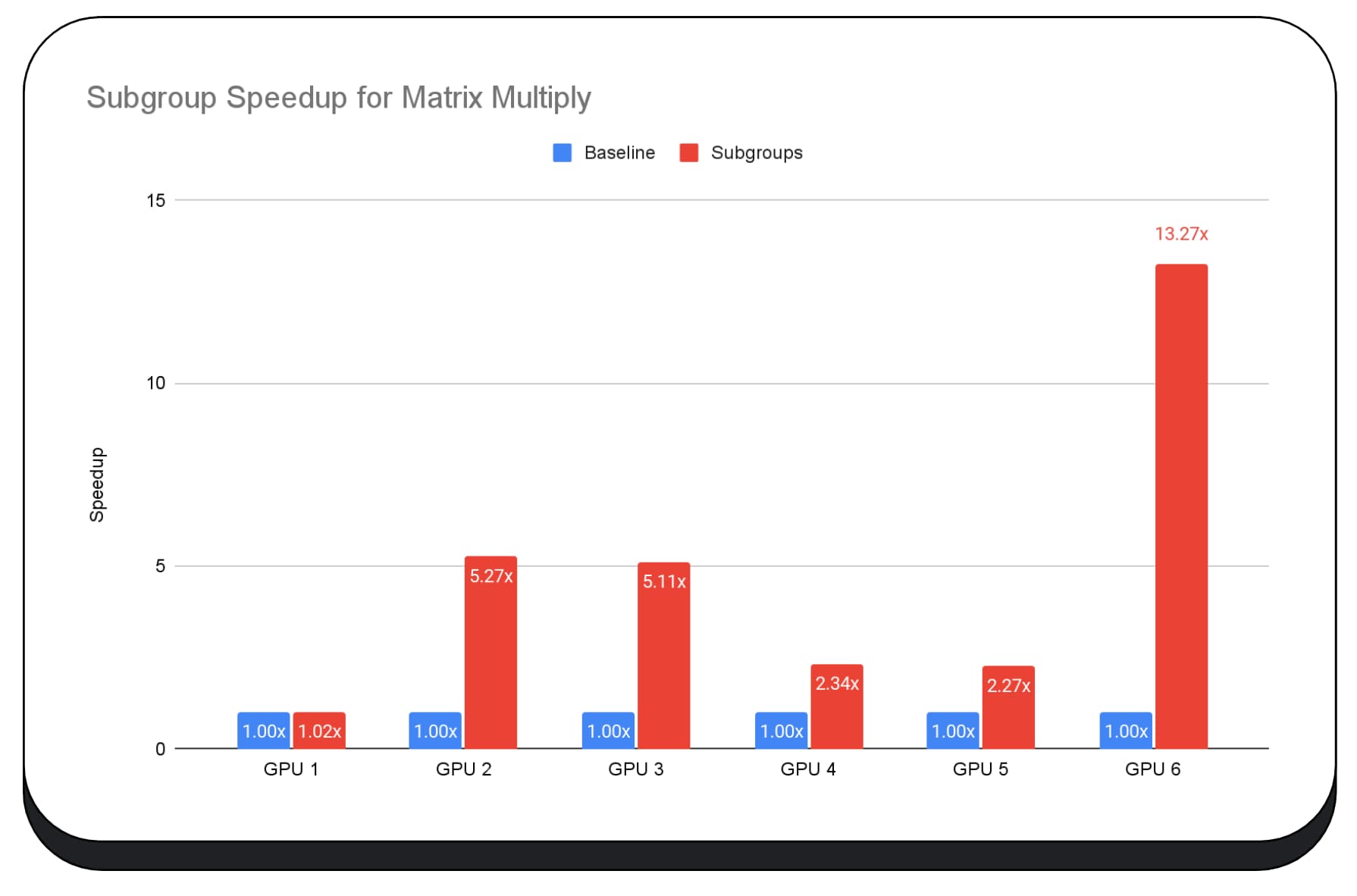
La optimización de la GPU es difícil
En última instancia, la mejor manera de optimizar tu GPU depende de la GPU que ofrezca el cliente. El uso de funciones nuevas y sofisticadas de la GPU no siempre es tan rentable como podrías esperar, ya que pueden intervenir muchos factores complejos. Es posible que la mejor estrategia de optimización en una GPU no sea la mejor estrategia en otra.
Quieres minimizar el ancho de banda de la memoria y, al mismo tiempo, usar por completo los subprocesos de procesamiento de la GPU.
Los patrones de acceso a la memoria también pueden ser muy importantes. Las GPUs suelen tener un mejor rendimiento cuando los subprocesos de procesamiento acceden a la memoria en un patrón que es óptimo para el hardware. Importante: Debes esperar diferentes características de rendimiento en el hardware de diferentes GPUs. Es posible que debas ejecutar diferentes optimizaciones según la GPU.
En el siguiente gráfico, tomamos el mismo algoritmo de multiplicación de matrices, pero agregamos otra dimensión para demostrar mejor el impacto de varias estrategias de optimización, y la complejidad y la variación entre diferentes GPUs. Presentamos una nueva técnica, que llamaremos "Swizzle". Swizzle optimiza los patrones de acceso a la memoria para que sean más óptimos para el hardware.
Puedes ver que el intercambio de memoria tiene un impacto significativo; a veces, incluso es más impactante que los subgrupos. En la GPU 6, el intercambio proporciona una aceleración de 12 veces, mientras que los subgrupos proporcionan una aceleración de 13 veces. En conjunto, tienen una increíble aceleración de 26 veces. En el caso de otras GPUs, a veces, la combinación de los subgrupos y el intercambio de subgrupos funciona mejor que cualquiera de ellos por separado. En otras GPUs, el uso exclusivo de swizzle ofrece el mejor rendimiento.
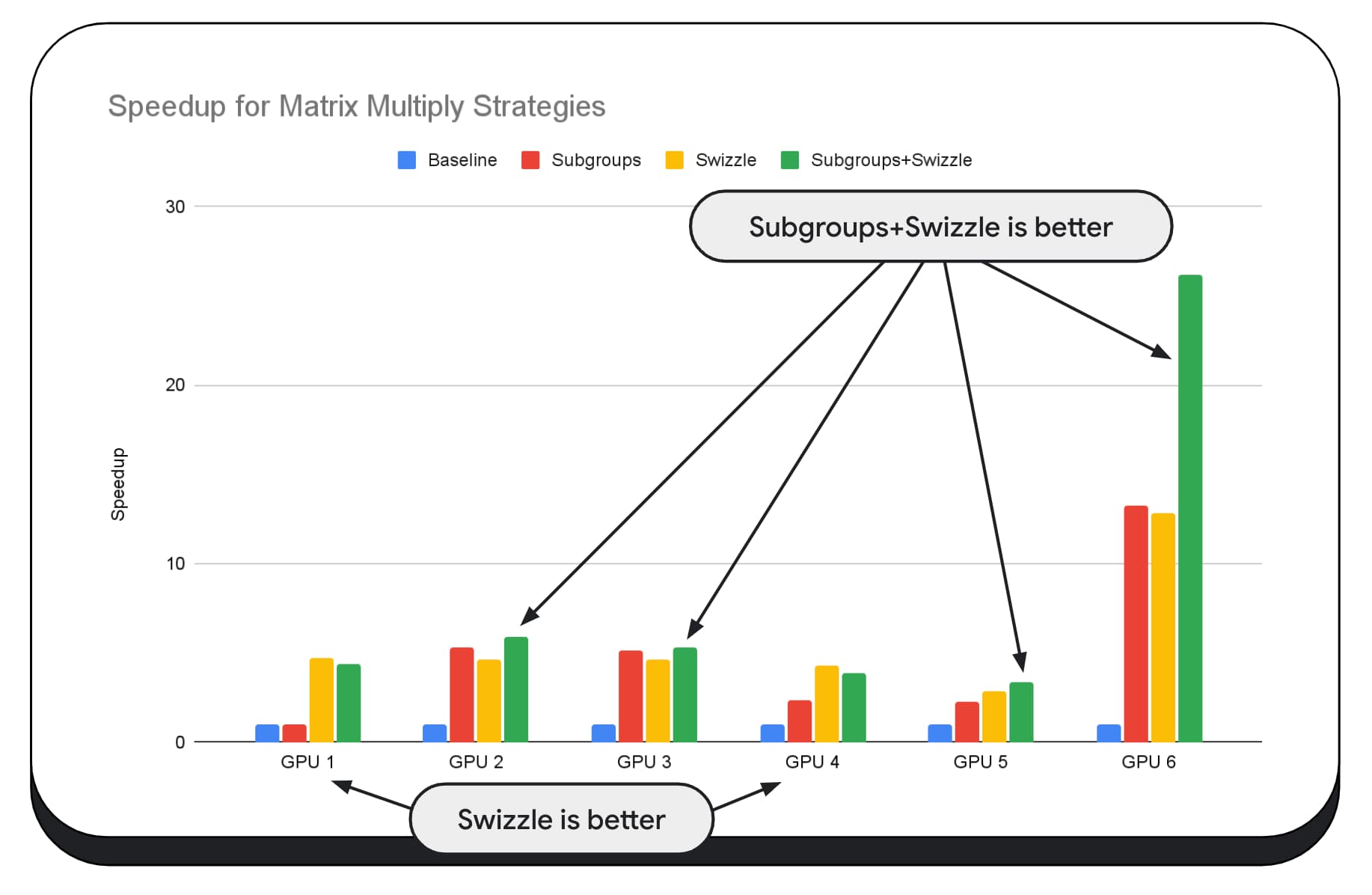
Ajustar y optimizar los algoritmos de la GPU para que funcionen bien en cada componente de hardware puede requerir mucha experiencia. Pero, por fortuna, hay una gran cantidad de trabajo talentoso en los frameworks de bibliotecas de nivel superior, como Mediapipe, Transformers.js, Apache TVM, ONNX Runtime Web y mucho más.
Las bibliotecas y los frameworks están bien posicionados para manejar la complejidad de administrar diversas arquitecturas de GPU y generar código específico de la plataforma que se ejecutará bien en el cliente.
Conclusiones
El equipo de Chrome sigue ayudando a desarrollar los estándares de WebAssembly y WebGPU para mejorar la plataforma web para las cargas de trabajo de aprendizaje automático. Estamos invirtiendo en primitivas de procesamiento más rápidas, una mejor interoperabilidad entre los estándares web y nos aseguramos de que los modelos grandes y pequeños puedan ejecutarse de manera eficiente en todos los dispositivos.
Nuestro objetivo es maximizar las capacidades de la plataforma y, al mismo tiempo, conservar lo mejor de la Web: su alcance, usabilidad y portabilidad. Y no estamos solos. Estamos trabajando en colaboración con los otros proveedores de navegadores del W3C y muchos socios de desarrollo.
Esperamos que recuerdes lo siguiente mientras trabajas con WebAssembly y WebGPU:
- La inferencia de IA ahora está disponible en la Web y en todos los dispositivos. Esto ofrece la ventaja de ejecutarse en dispositivos cliente, como un costo de servidor reducido, una latencia baja y una mayor privacidad.
- Si bien muchas de las funciones que se analizan son relevantes principalmente para los autores del framework, tus aplicaciones pueden beneficiarse sin mucha sobrecarga.
- Los estándares web son fluidos y evolucionan, y siempre estamos buscando comentarios. Comparte los tuyos para WebAssembly y WebGPU.
Agradecimientos
Queremos agradecer al equipo de gráficos web de Intel, que fue fundamental para impulsar las funciones de producto punto de números enteros empaquetados y f16 de WebGPU. Queremos agradecer a los otros miembros de los grupos de trabajo de WebAssembly y WebGPU del W3C, incluidos los otros proveedores de navegadores.
Gracias a los equipos de IA y AA de Google y de la comunidad de código abierto por ser socios increíbles. Y, por supuesto, a todos nuestros compañeros de equipo que hacen posible todo esto.




